控制系统实践3 - 状态反馈与状态观测

经典控制在处理SISO系统上有较好的效果，不管是理论分析和设计方法都较为系统丰富。但实际的控制系统往往不止包含唯一的输入输出，例如电机的角度和速度都输系统的输出，这时候现代控制理论的状态空间方法将会发挥作用。本小节介绍基于状态空间模型的状态反馈、LQR、卡尔曼滤波等。

状态空间模型与状态反馈

考虑电机的动力学模型：

$$K_m\dot w(t)+K_fw(t)=K_ii(t)\\ \dot\theta(t)=w(t)$$

令状态变量$x=[\theta,w]^T$，控制量$u=i_a$，得到如下状态空间模型：

$$\dot x= \begin{bmatrix} \dot\theta\\\dot w \end{bmatrix}= \begin{bmatrix} 0 & 1\\ 0 & -\frac{K_f}{K_m} \end{bmatrix} \begin{bmatrix} \theta\\w \end{bmatrix}+ \begin{bmatrix} 0\\ \frac{K_i}{K_m} \end{bmatrix}i_a= Ax+Bu\\ y = \begin{bmatrix} 1 & 0 \end{bmatrix}\begin{bmatrix} \theta\\w \end{bmatrix}=Cx$$

在设计系统的控制器之前，首先考虑系统的能控性：

$$S= \begin{bmatrix} B & AB \end{bmatrix} = \begin{bmatrix} 0 & \frac{K_i}{K_m}\\ \frac{K_i}{K_m} & -\frac{K_fK_i}{K_m^2} \end{bmatrix}, \quad \text{rank}(S)=2$$

在此基础上，设计状态反馈：

$$u=-Kx$$

则有：

$$\dot x = Ax+Bu=(A-BK)x$$

💡 上面设计的控制器是将系统的状态变量控制到$\begin{bmatrix} 0 \\ 0 \end{bmatrix}$，对于跟踪指定输入问题，例如控制电机角度跟踪期望轨迹$r(t)$，做如下状态变换，反馈系统有相同的状态矩阵： $$ u=-K\left( \begin{bmatrix} 1\\0 \end{bmatrix}r-x \right)\\ \dot x = (A-BK)x+Bk_1r $$

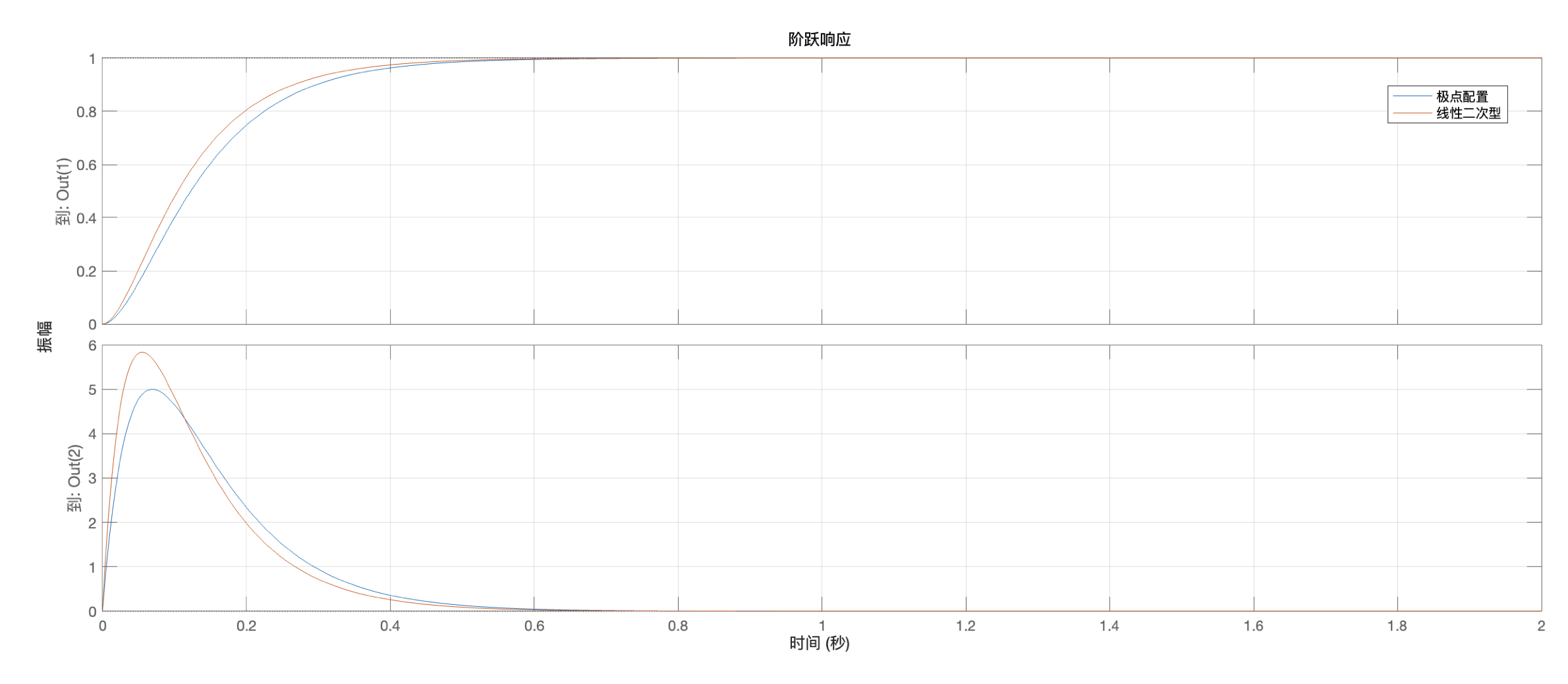
极点配置

状态空间模型表示系统的响应特性主要由状态矩阵的极点决定，因此可以通过配置(A-BK)的极点于期望的位置。若系统可控，则通过状态反馈，可以实现任意配置闭环系统极点的位置。在Matlab中可以通过如下代码来计算反馈增益矩阵：

A=[0,1;0,-7.2];B=[0;3000];
C=[1,0;0,1];D=[0;0];
ModelSS = ss(A,B,C,D);
poles = [-10,-20];
K1 = place(A,B,poles);

LQR - 线性二次型调节器

另一种设计反馈增益矩阵的方法，是通过构造控制代价函数，通过优化求解最优的增益矩阵。在实际的工程应用中，我们希望控制系统在跟踪误差、响应速度、输入能耗等各方面能有一个综合考虑，因此构造如下的代价函数（指标泛函）：

$$J=\int_0^\infty x^TQx+u^TRu\ dt$$

代价函数的含义是，当系统存在一个初始扰动x(0)时，将系统状态控制到原点过程中，状态误差和控制输出的总体评估。其中Q，R为权重矩阵，通常使用对角阵，在应用时往往根据工程需要和设计经验来确定。在Matlab中可以通过如下代码来计算LQR控制器的反馈增益矩阵：

A=[0,1;0,-7.2];B=[0;3000];
C=[1,0;0,1];D=[0;0];
ModelSS = ss(A,B,C,D);
Q = [0.01,0;0,0.0001]; R = 1;
[K2,S,P] = lqr(ModelSS,Q,R);

通过如下代码可以对所设计的控制器进行验证：

CL_SS1 = ss(A-B*K1,B*K1(1),C,D);
CL_SS2 = ss(A-B*K2,B*K2(1),C,D);
linearSystemAnalyzer(CL_SS1,CL_SS2);

卡尔曼滤波

控制和观测是控制理论中的对偶问题。除了通过状态反馈构建反馈控制器，状态空间模型的另一个重要的应用是进行状态观测，并由此引出一种非常重要的算法-卡尔曼滤波[1]。鉴于已经存在的优秀入门资料[2,3]，本文不会深入介绍Kalman Filter的理论推导，而仅介绍其在M3508控制中的一些具体应用和技巧。

M3508电机的反馈信号包括电机的角度、角速度和电机电流，其中角度和电流是由编码器和电流传感器直接测量得到的，角速度则是由角度差分得到的，前面我们做速度控制时也发现电机转速有较大的噪声。由于我们能够测量到电机的电流，通过电机的动力学模型我们也可以估计电机的转速， 那是不是可以利用模型计算和实际测量，来得到得到更准确的电机转速呢？

首先考虑如下最简单的状态空间模型：

$$x=[w(t)],\quad u=i_a(t)\\ \dot x= \begin{bmatrix} -\frac{K_f}{K_m} \end{bmatrix}x+ \begin{bmatrix} -\frac{K_i}{K_m} \end{bmatrix}u=Ax+Bu\\ y= \begin{bmatrix} 1 \end{bmatrix}x =Cx$$

由于卡尔曼滤波一般处理离散系统，因此在Matlab中通过如下代码将连续系统变换为离散模型：

Ac = [-7.2]; Bc = [3000]; Cc = [1]; Dc = 0;
modelSSC = ss(Ac,Bc,Cc,Dc);
modelSSD = c2d(modelSSC,0.001)

得到如下离散状态空间模型：

$$x=[w(k)],\quad u=i_a(k)\\ x(k+1)= \begin{bmatrix} 0.9928 \end{bmatrix}x(k)+ \begin{bmatrix} 2.989 \end{bmatrix}u(k)\\ y(k)=\begin{bmatrix} 1 \end{bmatrix}x(k)$$

由于电机角速度存在一定的测量噪声，建立的模型也存在一定的不确定性，因此考虑如下关系：

$$x(k+1)= Ax(k)+ Bu(k)+\text{w}(k)\\ y(k)=Cx(k)+\text{v}(k)$$

其中第一个式子的$\text{w}(k)$表示模型的误差，第二个式子的$\text{v}(k)$表示速度测量时的噪声。

当我们已知第k个时刻电机的速度$x(k)$和控制电流$u(k)$，并在第k+1个时刻测量到带有噪声的电机转速$y(k+1)$，那么可以把两者加权平均，得到k+1时刻更准确的速度估计$\hat x(k+1)=\alpha[Ax(k)+Bu(k)]+(1-\alpha)y(k+1)$。下面通过卡尔曼滤波来实现这一过程。

状态预测：

$$\hat x(k+1|k)=A\hat x(k|k)+Bu(k)\\ P(k+1|k)=AP(k|k)A^T+Q$$

计算新息与增益矩阵：

$$\varepsilon(k+1)=y(k+1)-C\hat x(k+1|k)\\ K(k+1)=P(k+1|k)C^T[CP(k+1|k)C^T+R]^{-1}$$

状态更新：

$$\hat x(k+1|k+1) =x(k+1|k)+K(k+1)\varepsilon(k+1)\\ P(k+1|k+1)=P(k+1|k)-K(k+1)CP(k+1|k)$$

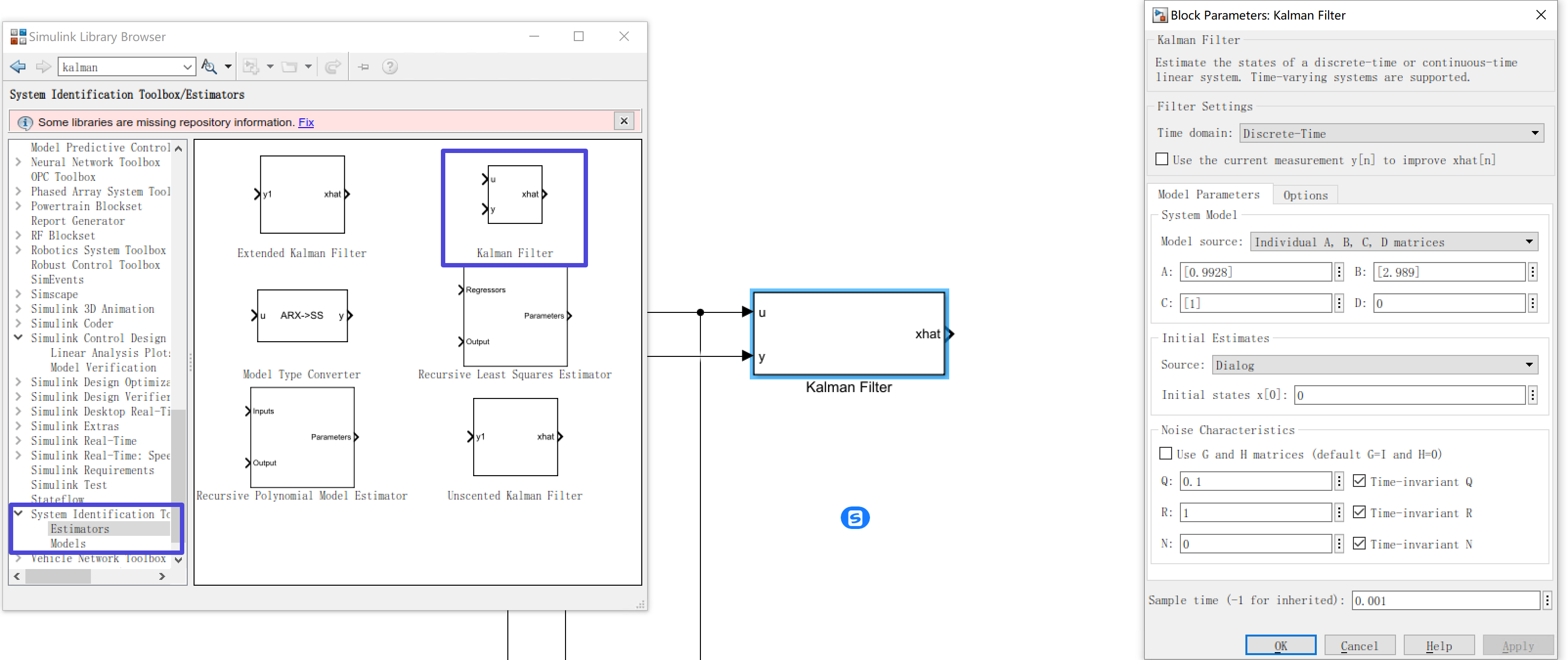
在dPSACE中我们通过如下代码实现卡尔曼滤波：

% 状态预测
X_k1k = A*X_kk + B*u;
P_k1k = A*P_kk*A'+Q;
% 计算新息
e_k1 = y-C*X_k1k;
K_k1 = (P_k1k*C')/(C*P_k1k*C'+R);
% 状态更新
P_kk = P_k1k-K_k1*C*P_kk;
X_kk = X_k1k + K_k1*e_k1;

其中u和y是外部输入，Q和R分别是w和v的协方差矩阵(一般为对角阵)，反应模型预测的不准确度和输出测量的噪声大小。当模型越不准确，Q应该取值越大；测量信号噪声越大，R应当越大，设计应用时需要根据经验进行调整，卡尔曼滤波的实际效果受这两个参数极大的影响。

我们还可以直接使用Simulink自带的卡尔曼滤波模块，Simulink提供了KF、EKF、UKF等多种形式的卡尔曼滤波器。但在Simulink代码生成时，自带的卡尔曼滤波不支持ControlDesk在线调参，没有自行编写的代码灵活。

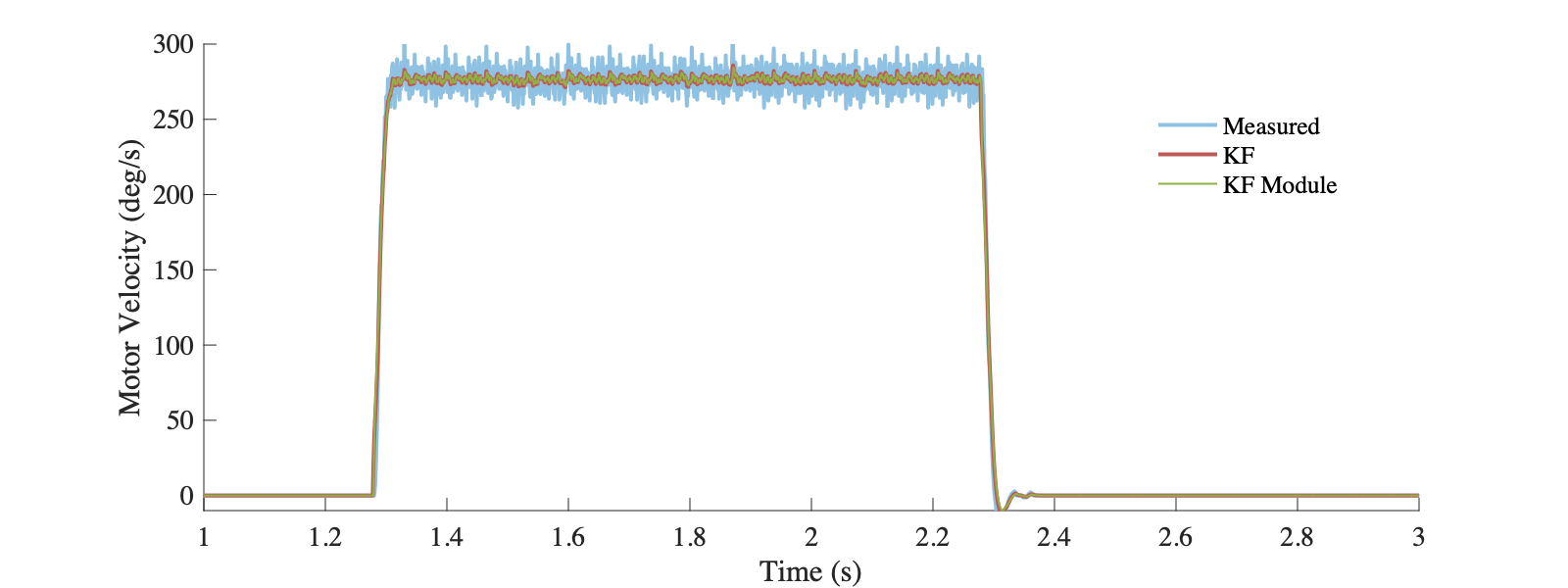
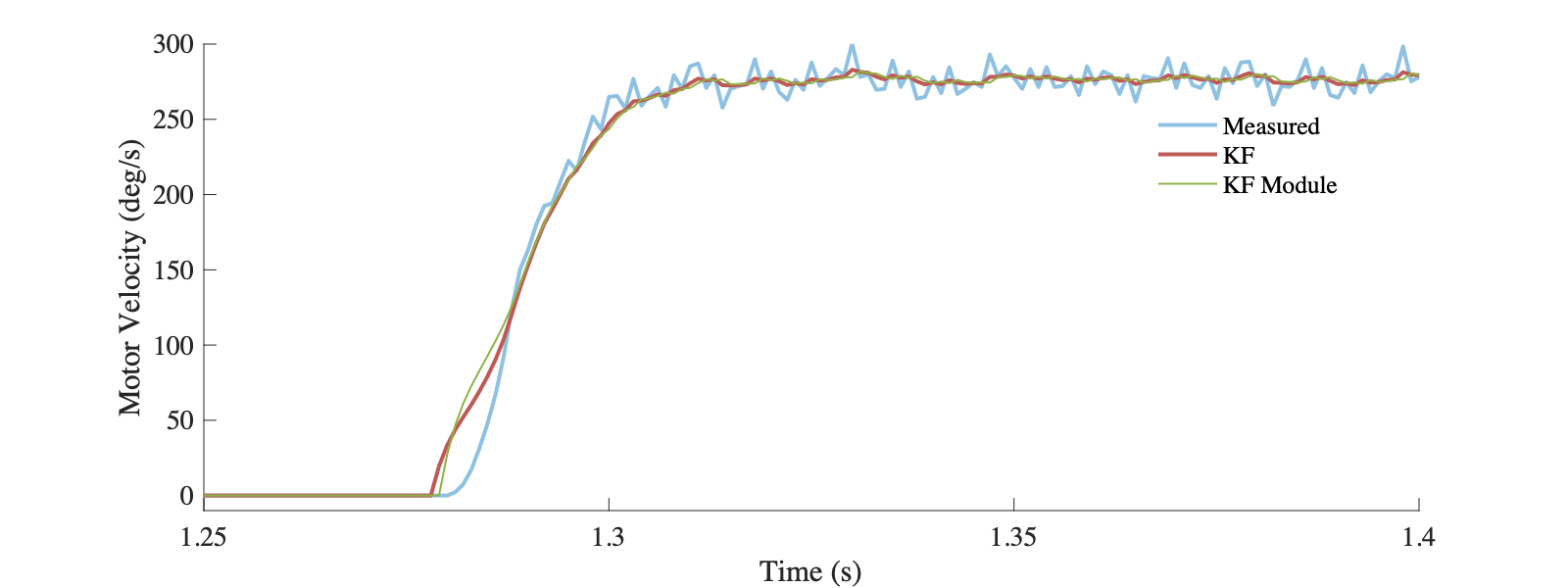
可以看到经过卡尔曼滤波后得到的电机速度更加平稳，并且滤波的数据并没有明显的延迟。这就是Kalman Filter的第一种用法 - 滤波(废话)。

数据融合

在前面的实验中我们发现不仅测量的电机速度有较大的噪声，电流的噪声也较大，这是由于电流传感器本身的测量特性。观察到我们的模型同时包含电机转速和电机电流，那能否同时利用测量的转速和电流，来得到更准确的输出？

为此，我们需要将电流也看作是一个状态变量而非控制量，考虑如下状态空间模型：

$$x=[w(t),i_a(t)]^T\\ \dot x= \begin{bmatrix} \dot w \\ \dot {i_a} \end{bmatrix} = \begin{bmatrix} -\frac{K_f}{K_m} & \frac{K_i}{K_m}\\ 0 & 0 \end{bmatrix} \begin{bmatrix} w \\ {i_a} \end{bmatrix} =Ax\\ y= \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}x =Cx$$

这里我们假设$\dot{i_a}=0$，因为电机电流本身是一个控制量，由我们设计的控制器产生，在没有其他信息的情况下我们只能假设其状态不变，并被测量到的结果所修正。

同样将系统转换为离散模型，使用上面相同的卡尔曼滤波器框架，并调整模型参数、输入数据和参数矩阵Q、R。注意这里的Q和R将从前面的标量变为二维矩阵(一般为对角阵)。

% 模型离散化
Ac = [-7.2,3000;0,0]; Bc = [0]; Cc = [1,0;0,1]; Dc = [0];
modelSSC = ss(Ac,Bc,Cc,Dc);
modelSSD = c2d(modelSSC,0.001)

%% kalman filter code
% 状态预测
X_k1k = A*X_kk;
Y_k1 = [vel;ia];
P_k1k = A*P_kk*A'+ diag(Q);
% 计算新息
e_k1 = Y_k1 - C*X_k1k;
K_k1 = (P_k1k*C')/(C*P_k1k*C'+ diag(R));
% 状态更新
X_kk = X_k1k + K_k1*e_k1;
P_kk = P_k1k-K_k1*C*P_kk;

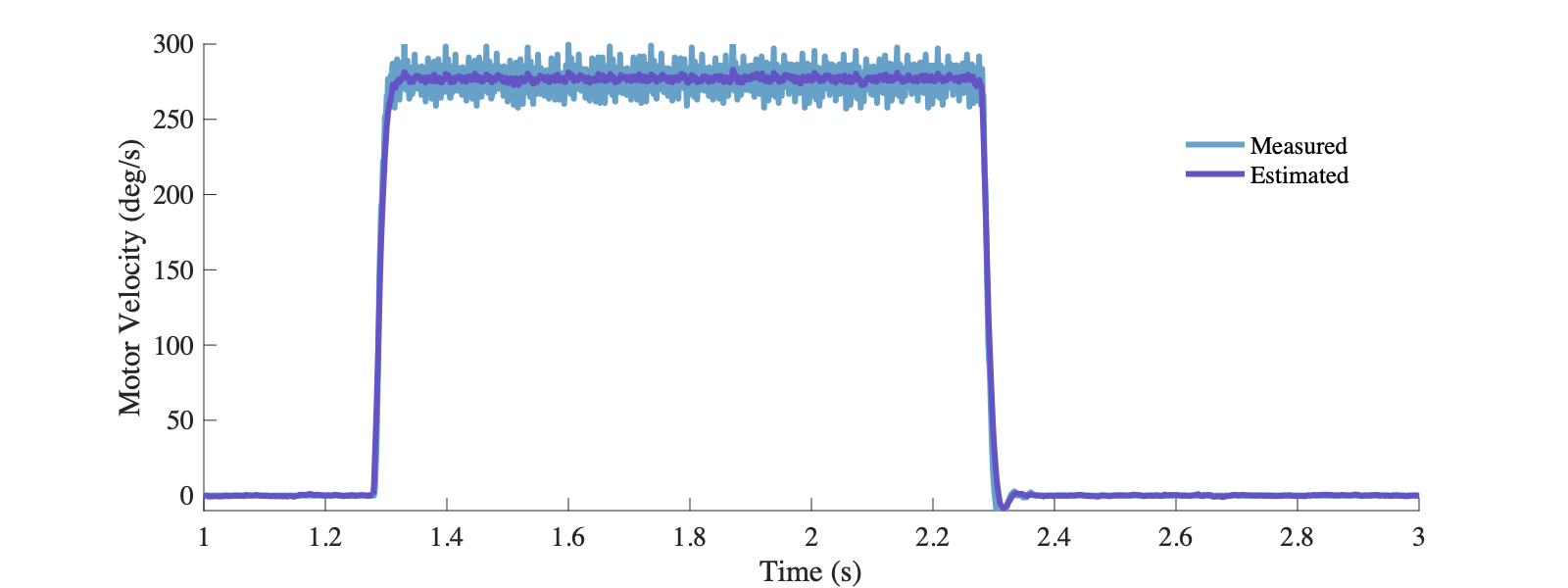
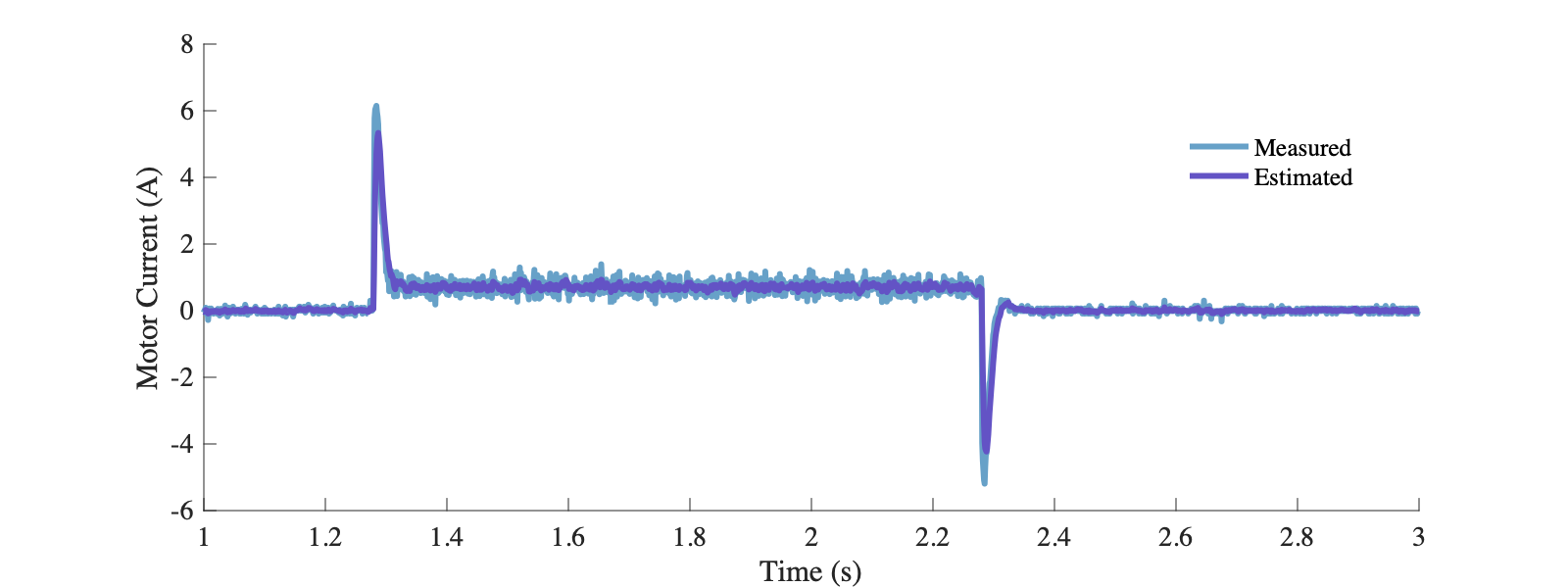
可以看出经过卡尔曼滤波后，电机速度和电流的估计比原始测量的结果都有更小的噪声。在这个过程中，我们综合利用了多种传感器的数据来得到更准确的估计，这种手段一般被称为数据融合，也是卡尔曼滤波非常常见的一种用法。在这篇博客[4]中介绍了使用IMU的加速度的和角速度信息，数据融合得到姿态角度的方法。

状态观测与估计

上面两个案例中，系统的状态都可以直接被观测到（也就是被传感器测量到），通过模型或数据融合得到更准确的估计。当有一些状态无法直接测量时，能否通过Kalman Filter进行估计呢？考虑前面电机模型，电机转动时若受到一个外力作用，能否能把外力的大小估计出来？考虑如下的动力学模型，其中$\tau_{ext}$为外部作用力：

$$K_m\dot w(t)+K_fw(t)=K_ii(t)+\tau_{ext}$$

构造如下的状态空间模型：

$$x=[w(t),i_a(t),\tau_{ext}(t)]^T\\ \dot x= \begin{bmatrix} \dot w \\ \dot {i_a} \\ \dot \tau_{ext} \end{bmatrix} = \begin{bmatrix} -\frac{K_f}{K_m} & \frac{K_i}{K_m} & \frac{1}{K_m}\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} w \\ {i_a} \end{bmatrix} =Ax\\ y= \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix}x =Cx$$

其中$\tau_{ext}$作为外部作用力，同样假设为恒定不变。将系统离散化后，采用相同的方法实现卡尔曼滤波。为测试估计效果，我们为电机产生一个外部输入：

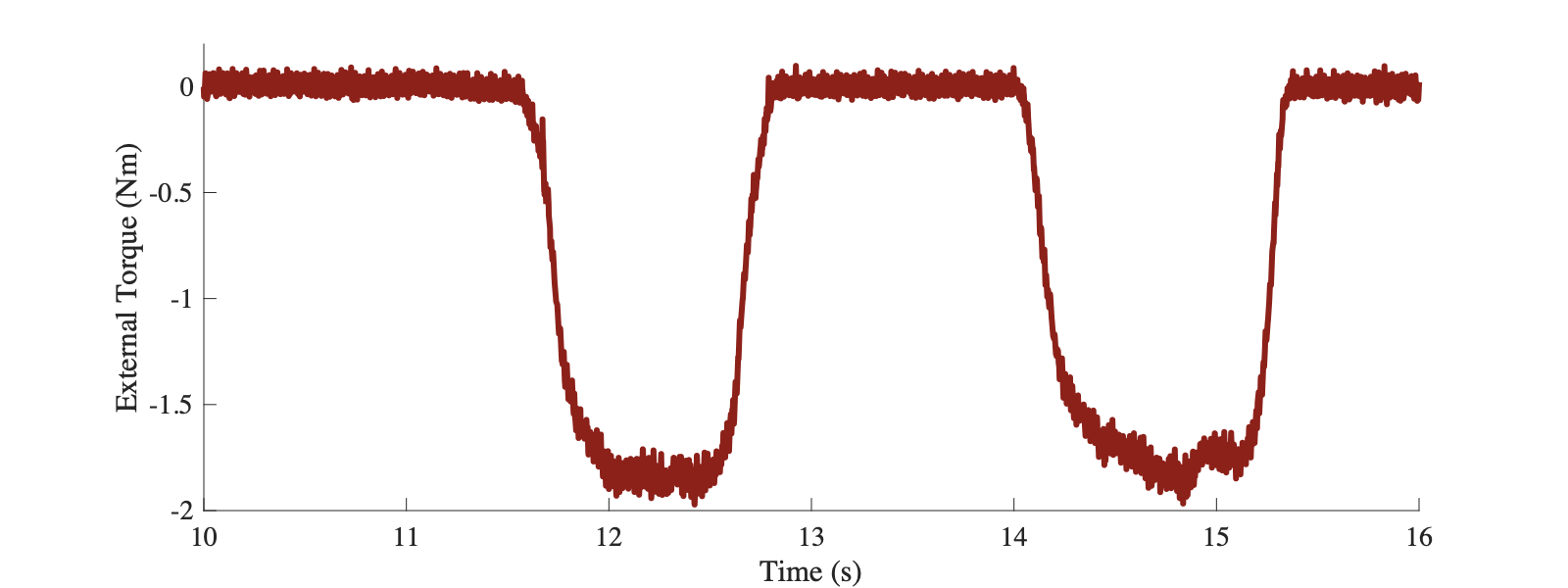
能看到算法实现了对外部扭矩的估计。其实在多数未安装扭矩传感器的机械臂中，就是采用类似的方法实现对输出转矩的估计。这就是卡尔曼滤波的第三种用法 - 状态观测。

Reference

1. Kalman R E. A new approach to linear filtering and prediction problems[J]. 1960.
2. Faragher R. Understanding the basis of the kalman filter via a simple and intuitive derivation [lecture notes][J]. IEEE Signal processing magazine, 2012, 29(5): 128-132.
3. 图说卡尔曼滤波，一份通俗易懂的教程 - 知乎 (zhihu.com)
4. An Introduction for IMU 2 - IMU数据融合与姿态解算 | 萤火 (jychen.cn)