控制系统实践2 - 基于经典控制的分析设计

从经典控制到现代控制，所有的控制算法的设计和分析都依赖于线性系统模型。在第一部分完成对系统模型的辨识后，本节我们介绍控制器设计和参数设计方法，并对M3508电机转速和位置进行控制。

速度控制 - 比例反馈

首先考虑最简单的反馈控制形式 - 比例控制，构建反馈控制回路后系统结构如下：

则闭环系统的传递函数为：

$\Phi(s)=\frac{k_pG(s)}{1+k_pG(s)}=\frac{3000k_p}{s+7.2+3000k_p}$

若控制器的设计需求为阶跃响应的稳态误差小于10%，调节时间小于0.1s，则可得到如下关系：

$K_0=\frac{3000k_p}{3000k_p+7.2}>0.9,\quad T_s=3T_m=\frac{3}{3000k_p+7.2}<0.1\\ \Rightarrow\ k_p>0.0216,\quad k_p>0.0076$

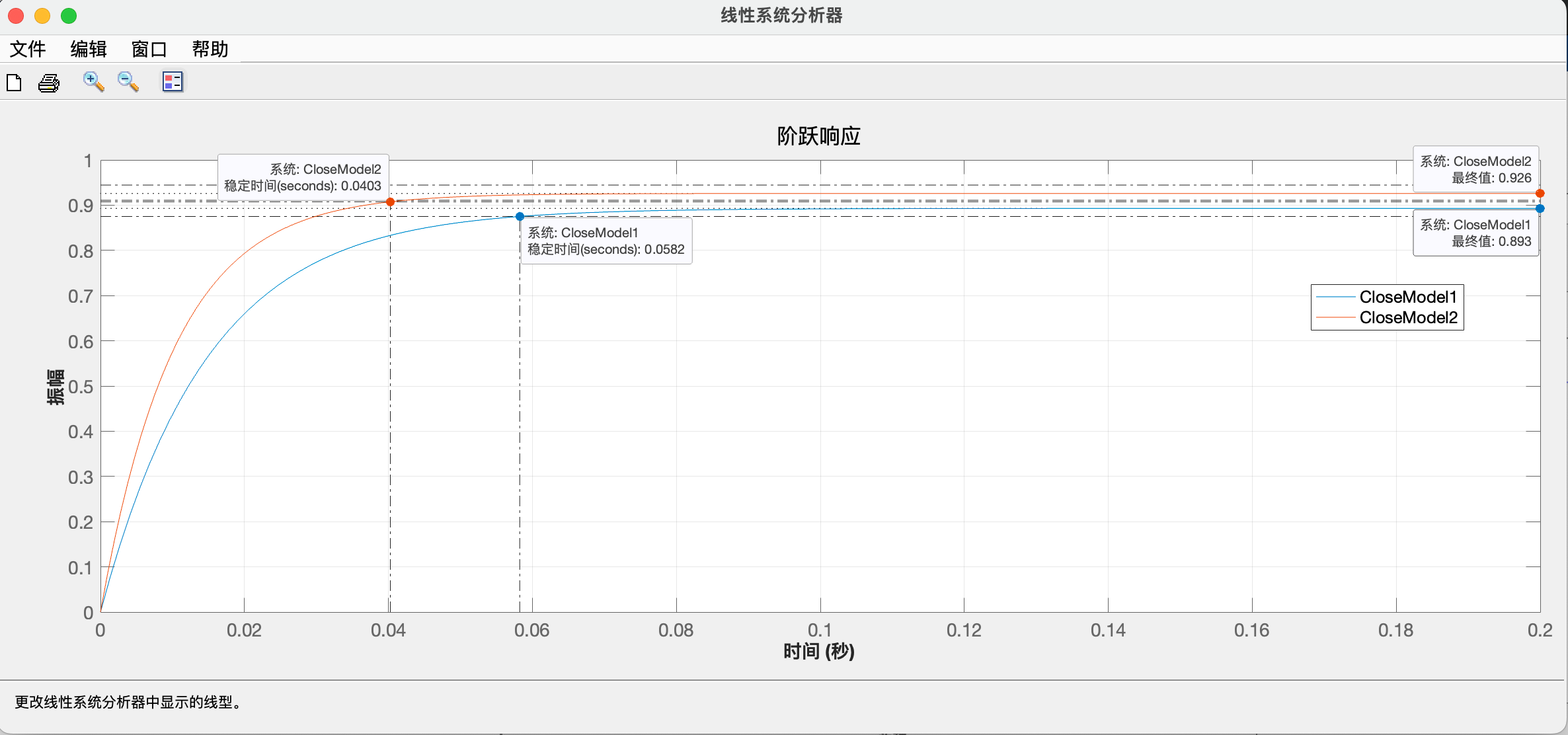
若取$k_p=0.02$，则$\Phi_1(s)=\frac{60}{s+67.2}$，调节时间=0.0582s，单位阶跃响应的稳态值为0.893；

若取$k_p=0.03$，则$\Phi_2(s)=\frac{90}{s+97.2}$，调节时间=0.0402s，单位阶跃响应的稳态值为0.926；

对于SISO的线性系统，我们可以通过Matlab的控制系统设计工具箱来简化我们的设计和分析流程。通过以下代码打开SISO线性系统控制设计器：

1 2	Motor=tf([3000],[1 7.2]); controlSystemDesigner(Motor);

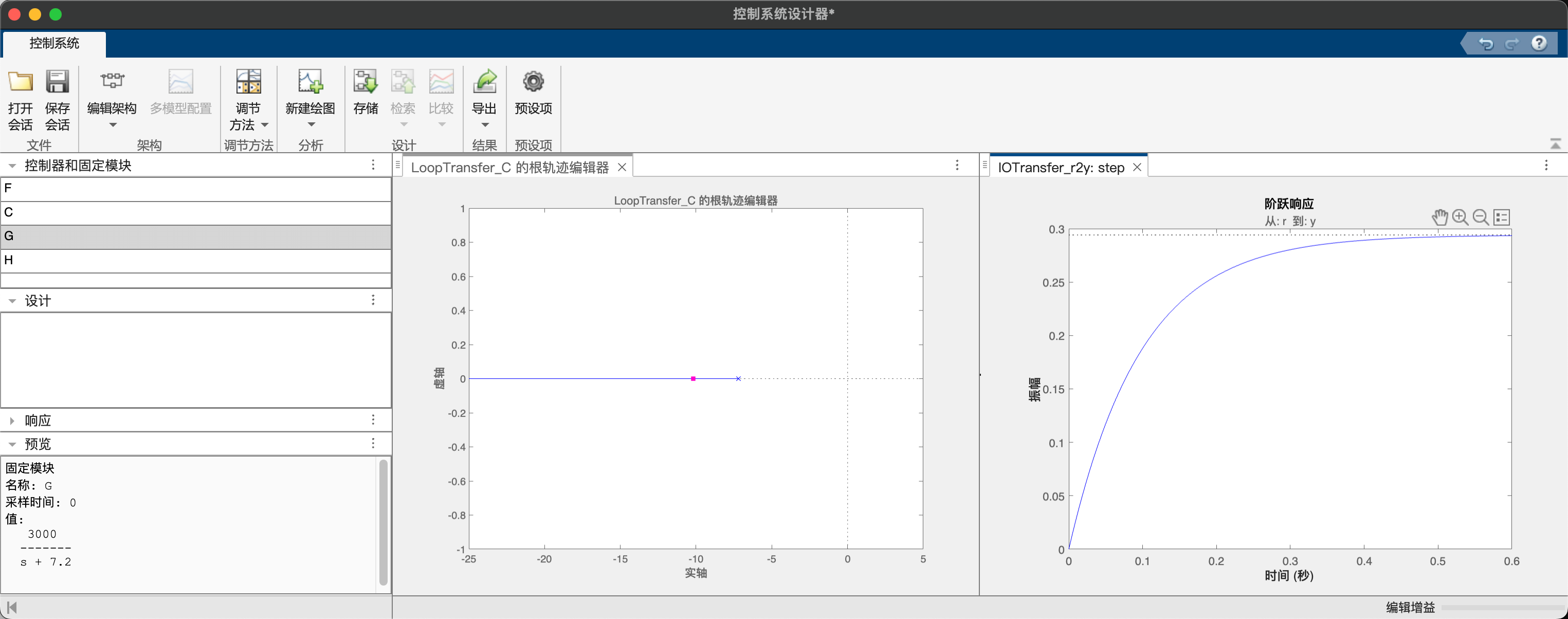
经典控制理论中对于SISO系统分析和设计的一个重要方法是根轨迹图。对于速度控制而言，其开环模型$\frac{3000k_p}{s+7.2}$仅有一个位于负实轴的极点，因此闭环系统的根轨迹$-7.2$由指向$-\infty$。在设计器中，我们可以通过拖拽闭环极点置于期望的位置（左图中红色的位置），并得到相应的控制器增益，在右侧可以看到所设计的闭环系统的单位阶跃响应。

对于设计好的控制器，我们可以通过线性系统分析器linearSystemAnalyzer，来分析系统的闭环响应。考虑上面所设计的闭环系统$\Phi_1,\Phi_2$，便携如下代码：

1
2
3

CloseModel1 = tf([60],[1 67.2]);
CloseModel2 = tf([90],[1 97.2]);
linearSystemAnalyzer(CloseModel1,CloseModel2);

在完成控制器设计后，我们通过实验对其进行验证。在dSPACE的主要代码如下：

1 2	error_vel = desired_vel - motor_vel; motor_cmd = KpVel * error_vel;

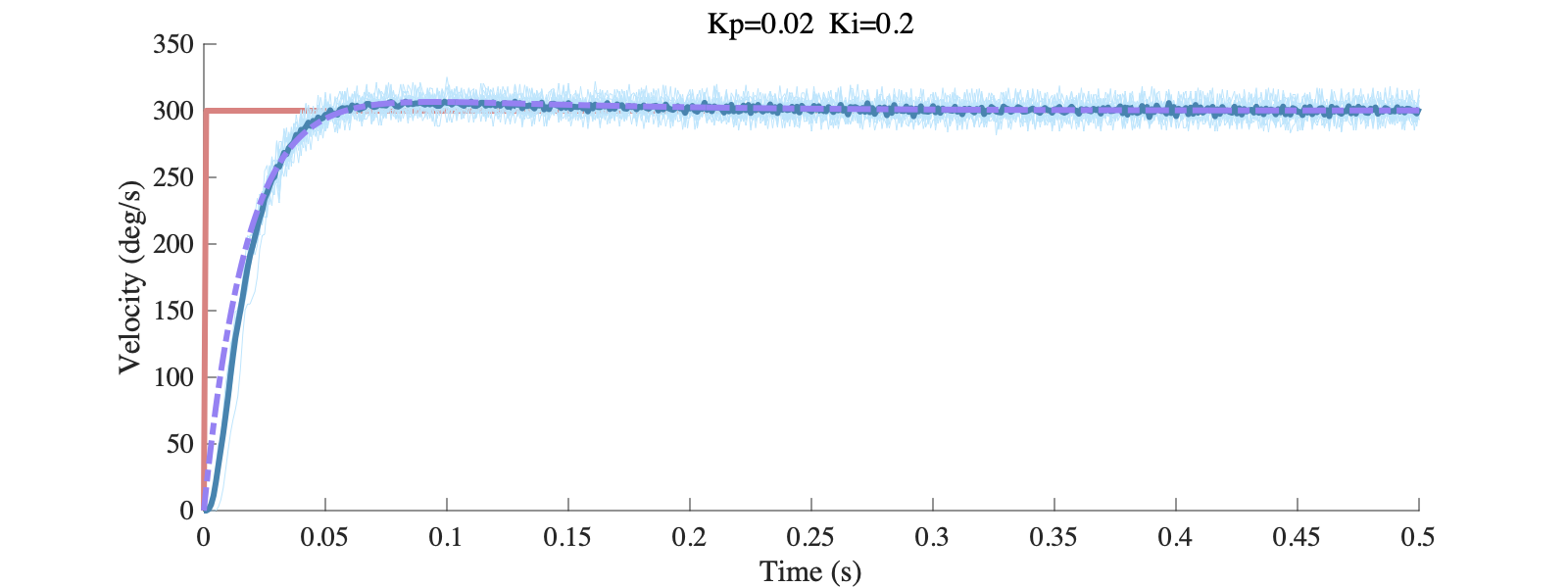
desired_vel为期望电机转速，本实验中设置幅值为300deg/s，两组参数下实验与仿真结果的对比如下图所示，红色曲线为期望转速，深蓝色曲线为多次阶跃响应的平均结果，紫色虚线为仿真结果：

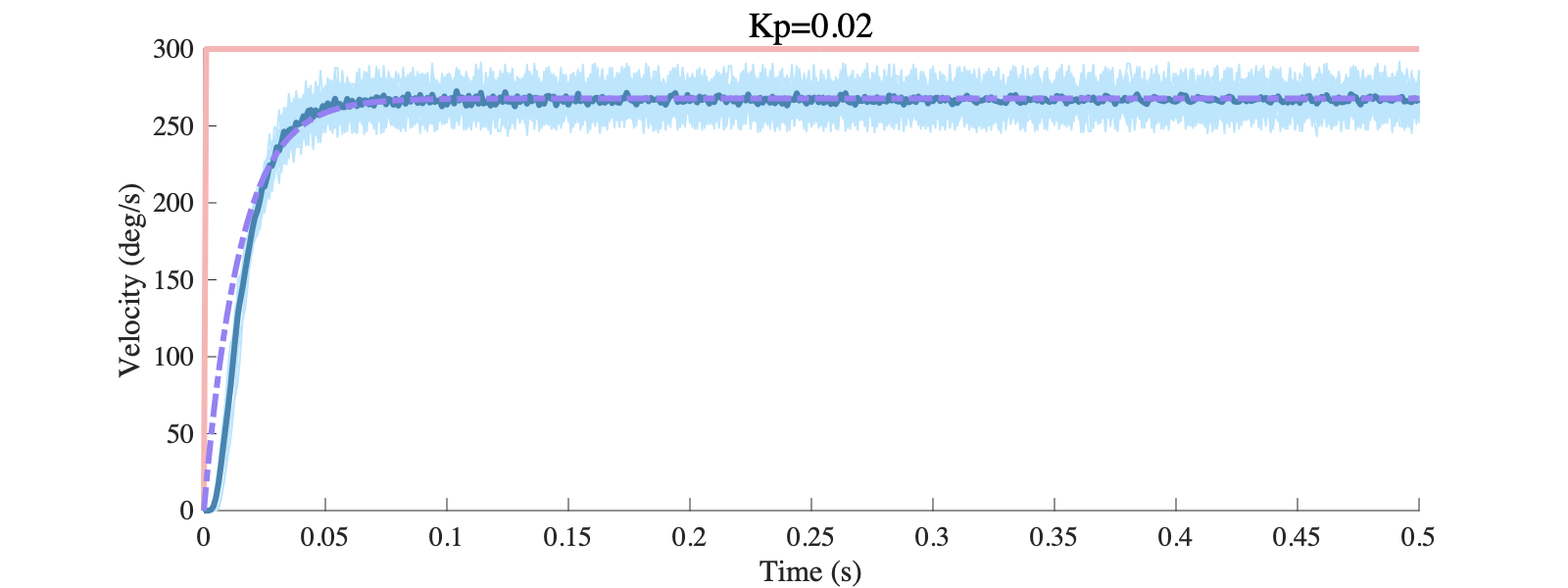
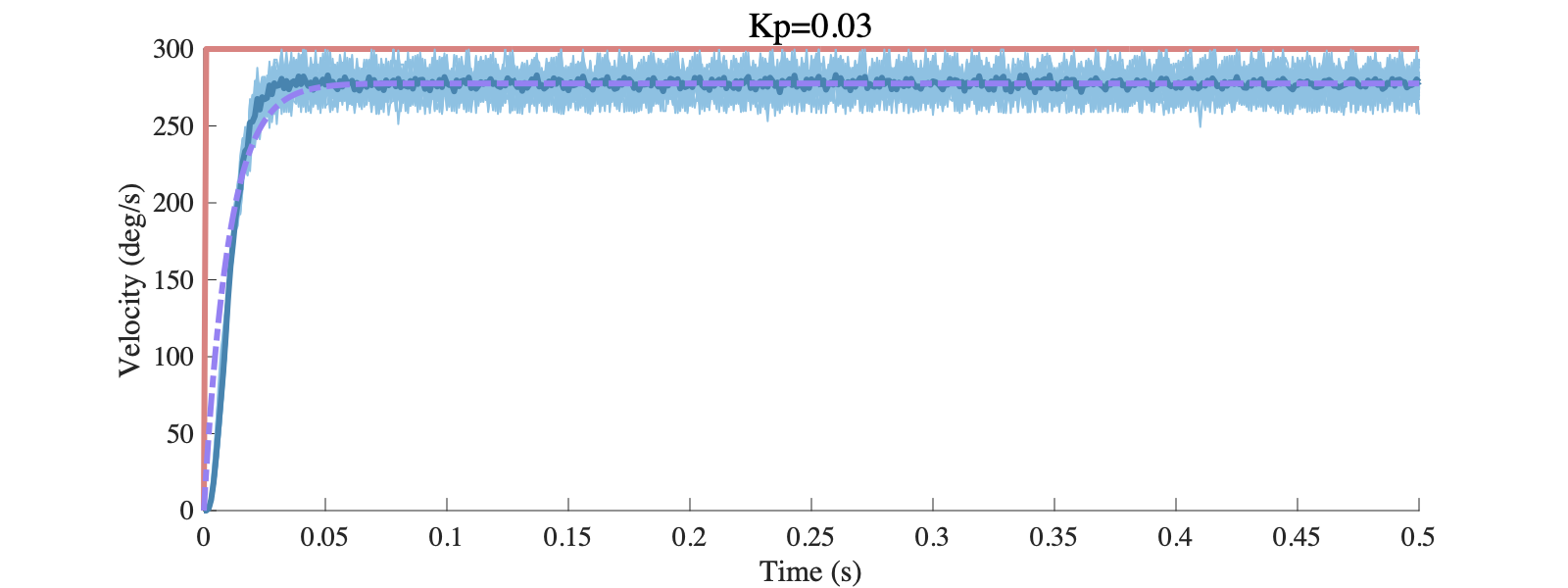
可以看出仿真和实验结果整体比较接近，尤其是稳态响应，但动态过程有一些差异，这个我们后面再进一步讨论。整体上来说，通过建模分析我们可以直接确定控制器的参数取值和闭环系统的响应特性，而不需要盲目的调整或试凑参数。

速度- 比例积分PI

由于电流-速度为一阶模型，在使用比例控制时始终会存在稳态误差，因此进一步考虑比例积分控制。

闭环系统的传递函数为：

$\Phi(s)=\frac{\frac{k_p+k_is}{s}G(s)}{1+\frac{k_p+k_is}{s}G(s)}=\frac{3000(k_ps+k_i)}{s^2+(7.2+3000k_p)s+3000k_i}$

开环系统的极点为$p_1=0,\ p_2-7.2$，开环零点为$z_1=-\frac{k_i}{k_p}$。

当$z_1=-\frac{k_i}{k_p}>-7.2$时，开环零点位于两个极点之间，因此根轨迹全部位于复实轴上，闭环系统一定具有欠阻尼的特性；取$z_1=-\frac{k_i}{k_p}=-\frac{0.1}{0.02}=-5$，则闭环系统为$\Phi(s)=\frac{60s+300}{s^2+67.2s+300}$。

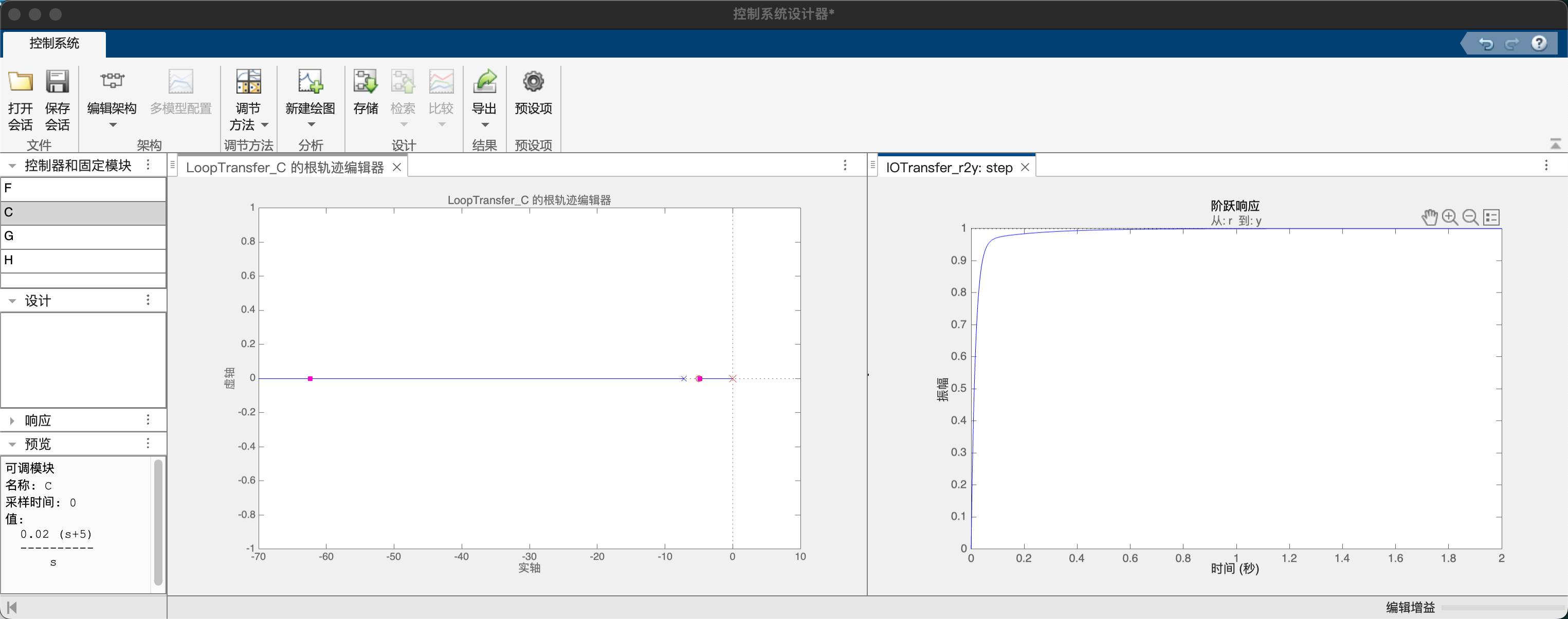
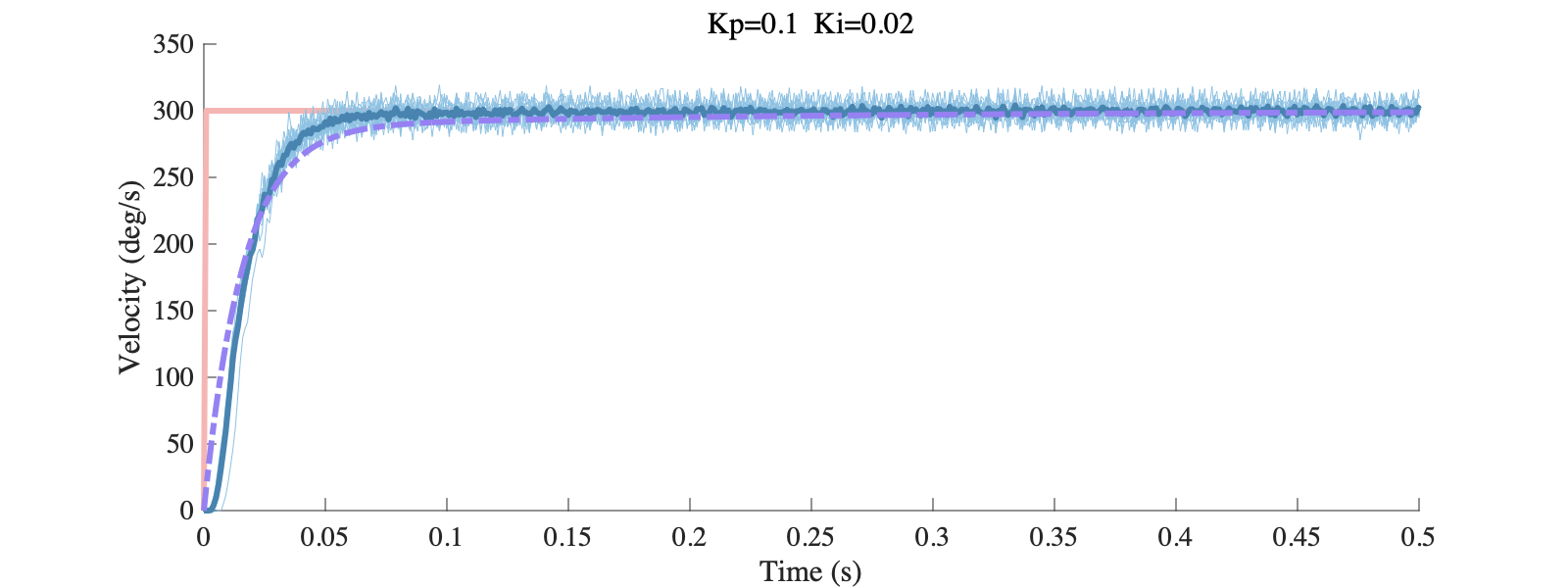
当$z_1=-\frac{k_i}{k_p}<-7.2$时，开环零点位于两个极点右侧，此时根轨迹先相交再分离，通过选取合适的增益，可以使闭环极点依然在负实轴上，同时有更快的响应速度。当$z_1=-\frac{k_i}{k_p}=-\frac{0.2}{0.02}=-10$，则闭环系统为$\Phi(s)=\frac{60s+600}{s^2+67.2s+600}$。

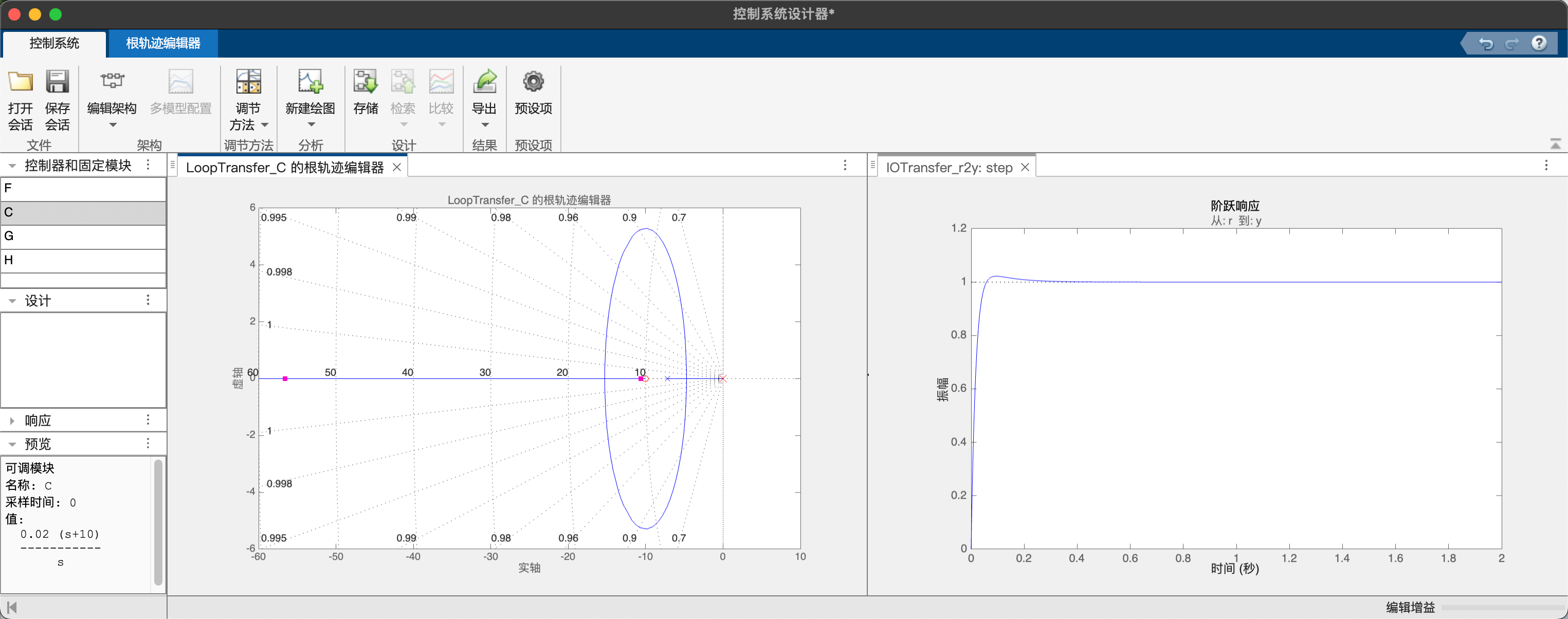
当根轨迹先相交再分离时，某些增益的取值会使得闭环系统存在一对共轭极点，系统呈现欠阻尼的特性；例如取$z_1=-\frac{k_i}{k_p}=-\frac{1}{0.02}=-50$，则闭环系统为$\Phi(s)=\frac{60s+3000}{s^2+67.2s+3000}$，系统的阶跃响应有明显的超调。

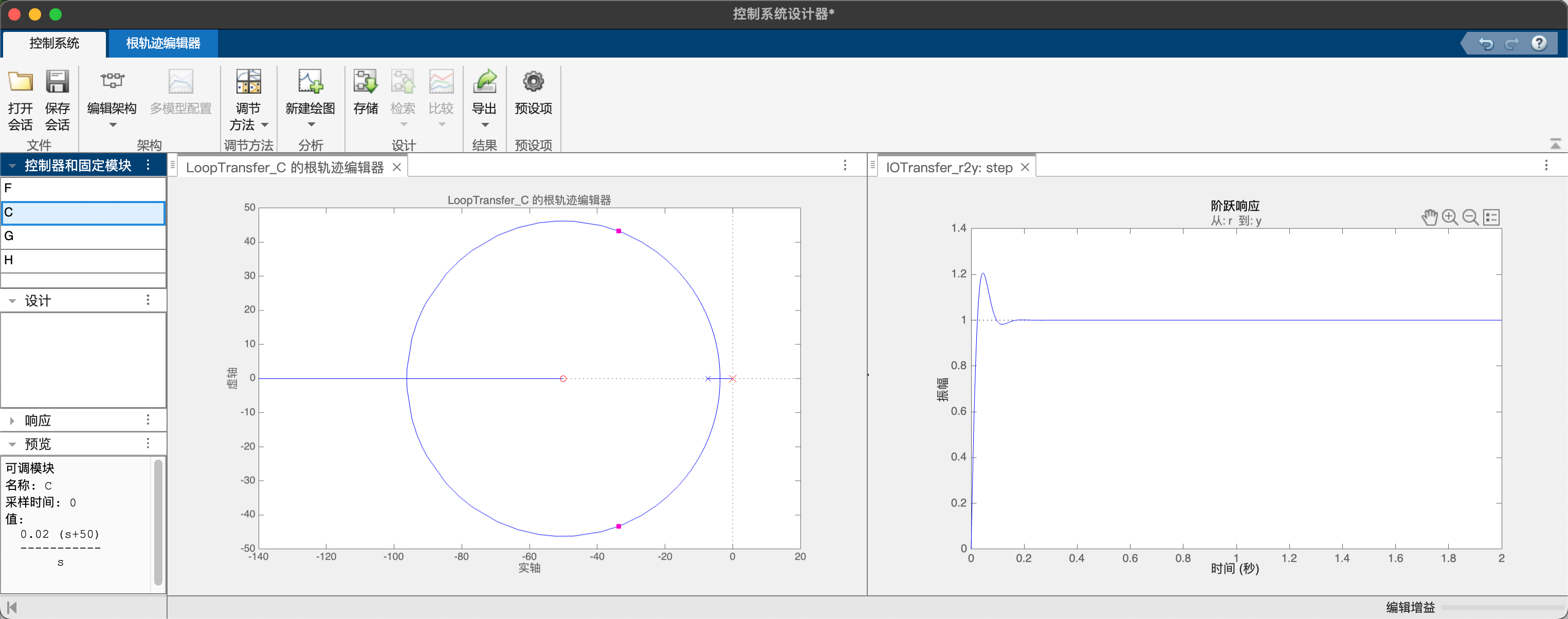
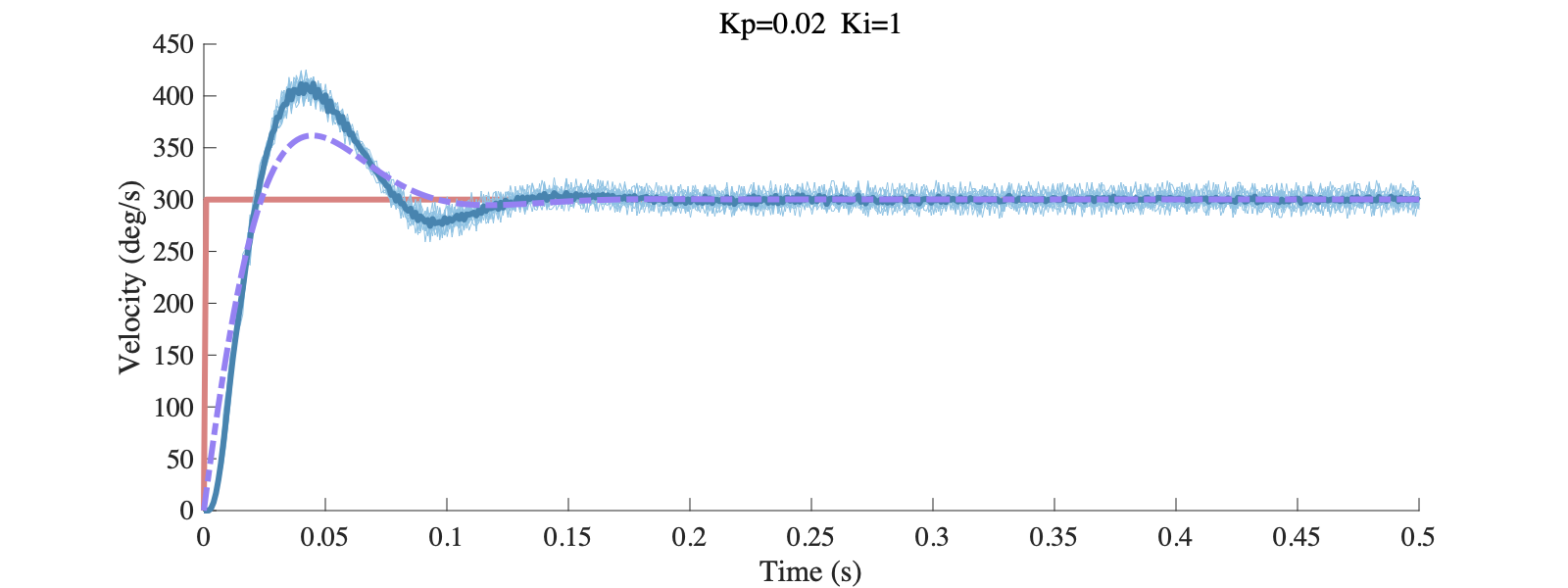
可以看出这组实验的超调远高于预测结果，在之前实验中仿真结果和实验结果也存在一定偏差。这主要是因为我们在建模的时候忽略系统的高频特性，在实际系统响应速度过快时，仿真模型和实际系统就有较大的偏差。对于所设计的控制器$C_{PI_3}(s)=\frac{0.02s+1}{s}$，对比前面辨识得到的一阶系统模型$G_1(s)=\frac{3000}{s+7.2}$和三阶系统模型$G_3(s)=\frac{3.461\times10^{8}}{s^3+380.9s^2+1.123\times10^5s+8.647\times10^5}$的阶跃响应差异，能够看出高阶模型的仿真结果更加接近实验。

Cpi= tf([0.02,1],[1 0]);
G1 = tf([3000],[1 7.2]); 
G3 = tf([3.461e08],[1,380.9,1.123e05,8.647e05]);
Phi1 = feedback(Cpi*G1,1);
Phi3 = feedback(Cpi*G3,1);
linearSystemAnalyzer(Phi1,Phi3);

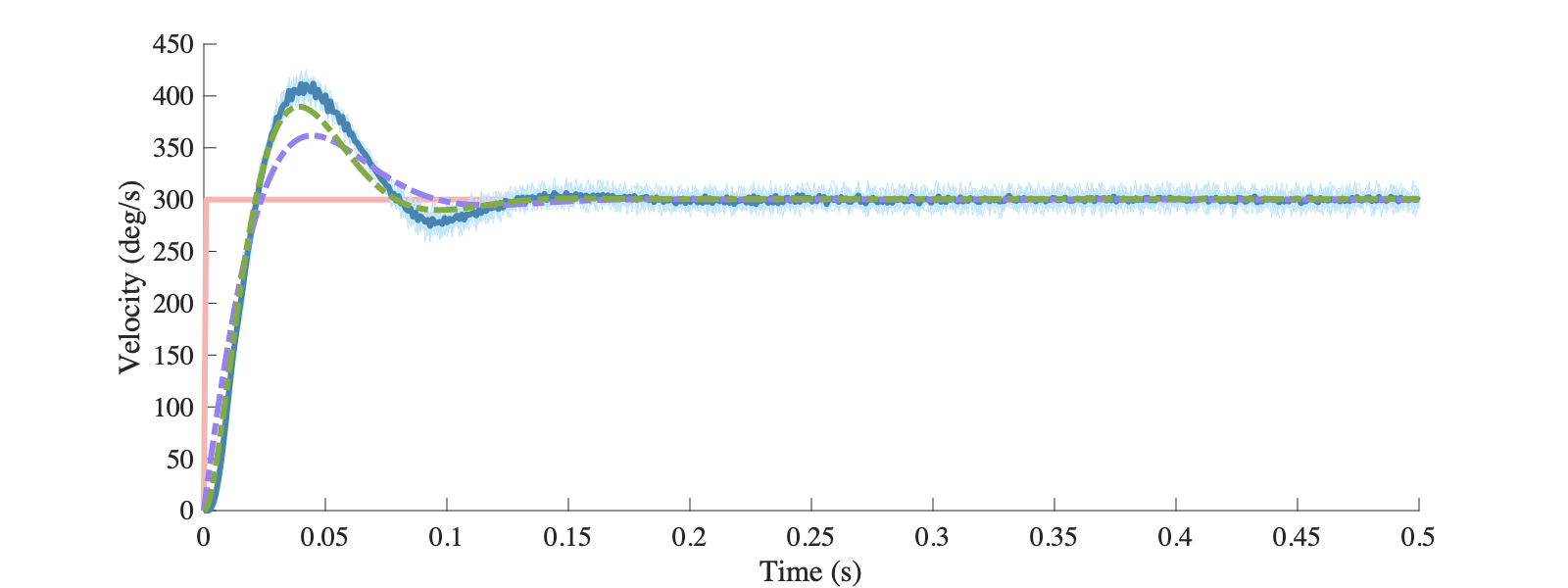
实际控制器设计时，我们并不希望系统有这样的超调，在选择$-\frac{k_i}{k_p}=-\frac{0.2}{0.02}=-10$时，系统不会有过快的动态响应，因此仿真结果也相对准确一些。

测度反馈

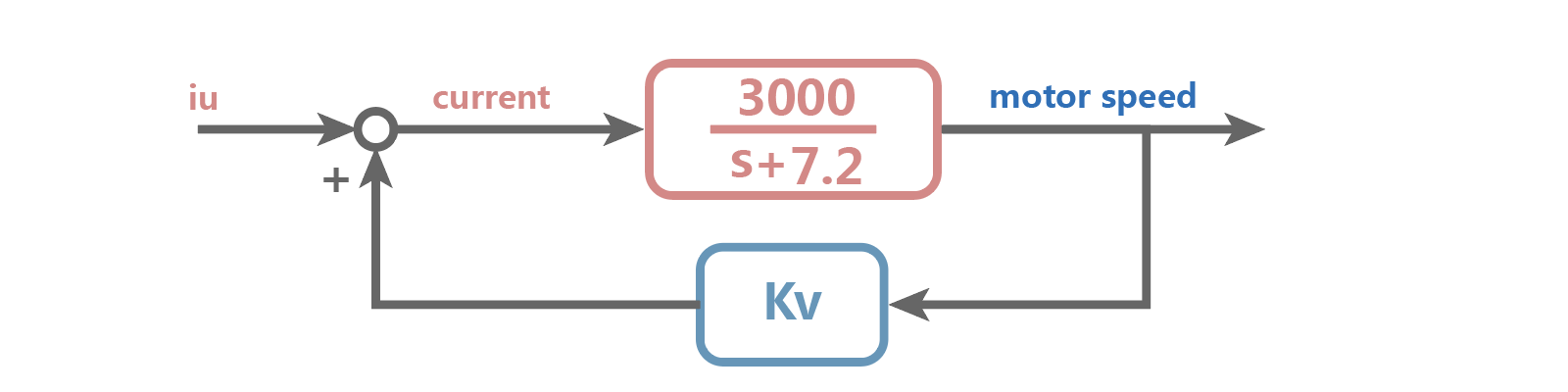
考虑上图的系统回路，电机转速通过增益后直接反馈至电机电流，系统的闭环模型为：

$\Phi(s)=\frac{G(s)}{1-k_vG(s)}=\frac{3000}{s+7.2-3000k_v}$

注意前面速度控制的闭环系统传递函数描述的是由期望速度到输出速度的关系$\Phi(s)=\frac{w(s)}{w_{des}(s)}$，而这里的传递函数描述的依然是电流到速度的关系$\Phi(s)=\frac{w(s)}{i_a(s)}$。速度反馈只是改变的系统的极点位置，而并没有构成反馈控制系统，因为这里并不存在一个期望转速。

将传递函数变换到时域，可得到反馈系统的动力学方程：

$\dot w(t)-(7.2-3000k_v)w(t)=3000i_u(t)$

或者我们考虑$i_a = i_u+K_vw$，结合系统的动力学方程$K_m\dot\omega+K_f\omega=K_ii_a$，则有：

$K_m\dot w(t)+(K_f-K_iK_v)w(t)=K_ii_u(t)$

速度反馈实际上改变了系统的阻尼或摩擦，改变了系统本身的特性，通过调整Kv可以使系统的阻尼减小，但要注意Kv<Kf/Ki，否则阻尼极性反转、反馈系统极点位于右半平面，系统将不稳定。

我们可以进一步通过反馈为系统增加一定的弹性，使其成为一般的弹簧阻尼系统，或者我们考虑$i_a = i_u+K_vw-K_c\theta$：

$K_m\ddot \theta(t)+(K_f-K_iK_v)\dot\theta(t)+K_c\theta=K_ii_u(t)$

注意这里我们构建速测反馈或角度反馈时没有任何的期望输入，控制电流$i_u$始终为0（但$i_a$不为零），反馈或者说补偿的引入，改变系统的动力学模型，后面我们还将进一步讨论这个问题。

位置控制 - 比例微分PD

下面我们考虑电机位置控制问题，由于转角是转速的积分，因此直接得到电流到角度的传递函数：

$G(s) = \frac{3000}{s(s+7.2)}$

首先考虑比例控制：

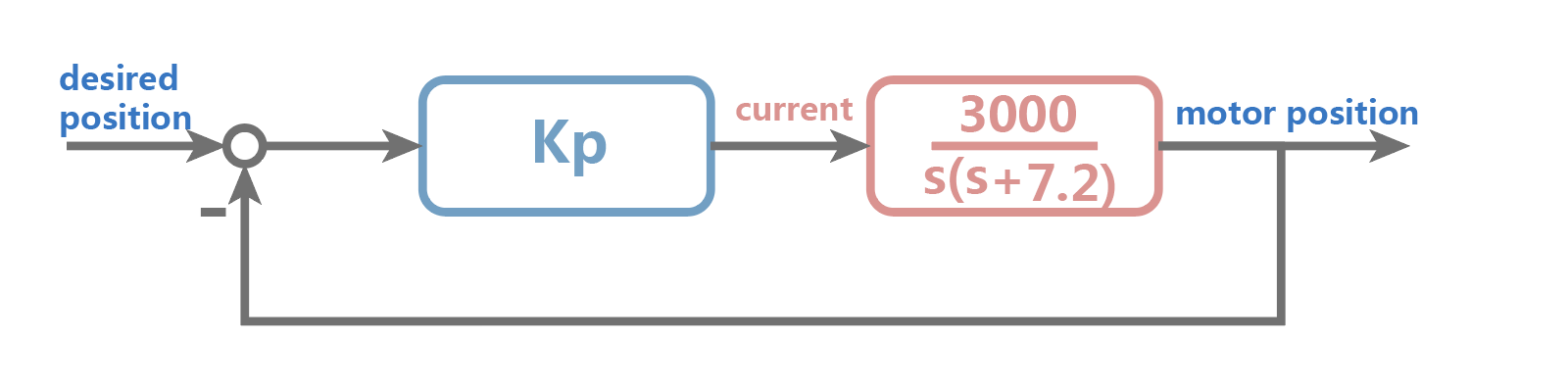
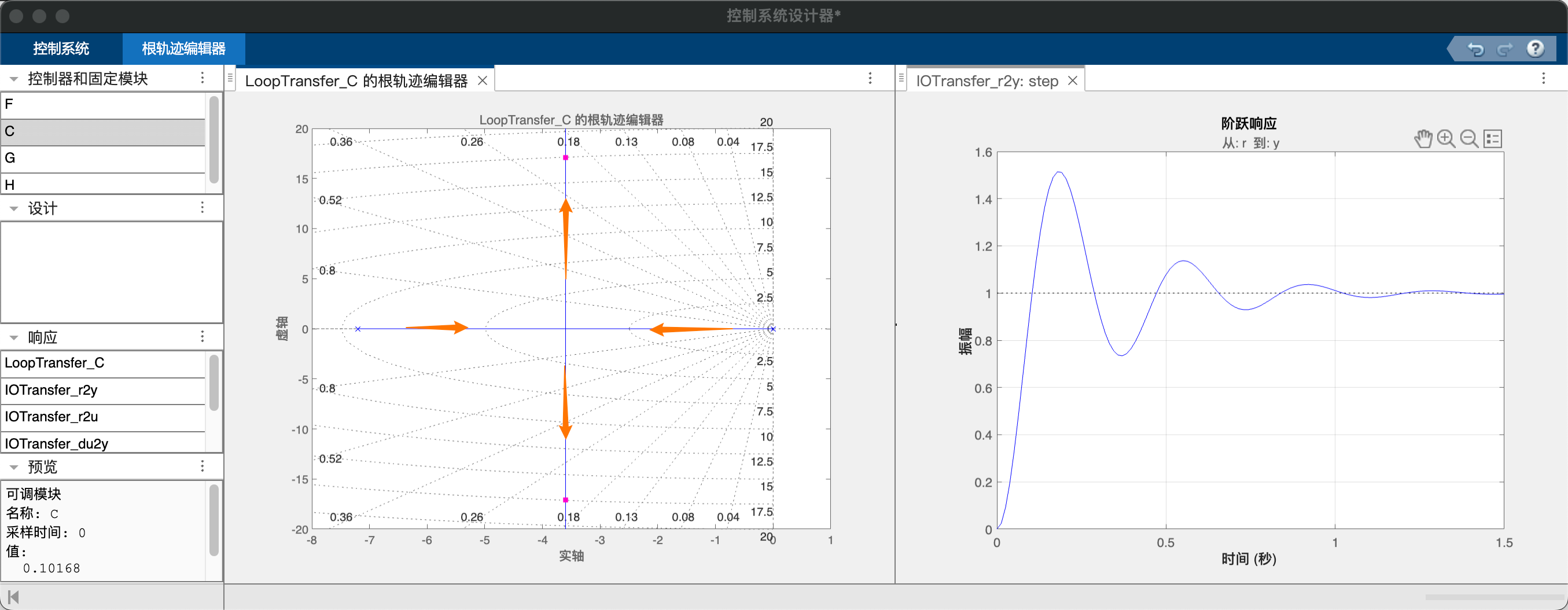
由于系统的开环极点位于0,-7.2，因此闭环系统的根轨迹在负实轴上汇合后发散到无穷远。单纯调节控制增益只能改变系统的阻尼，而无法改变响应时间（极点负实部的大小）。如果我们给系统增加一个小于-7.2的开环零点，则根轨迹能够被吸引到更远离实轴的位置，因此考虑比例微分控制：

$\Phi(s)=\frac{(k_p+k_ds)G(s)}{1+(k_p+k_ds)G(s)}=\frac{3000(k_p+k_ds)}{s^2+(7.2+3000k_d)s+3000k_p}$

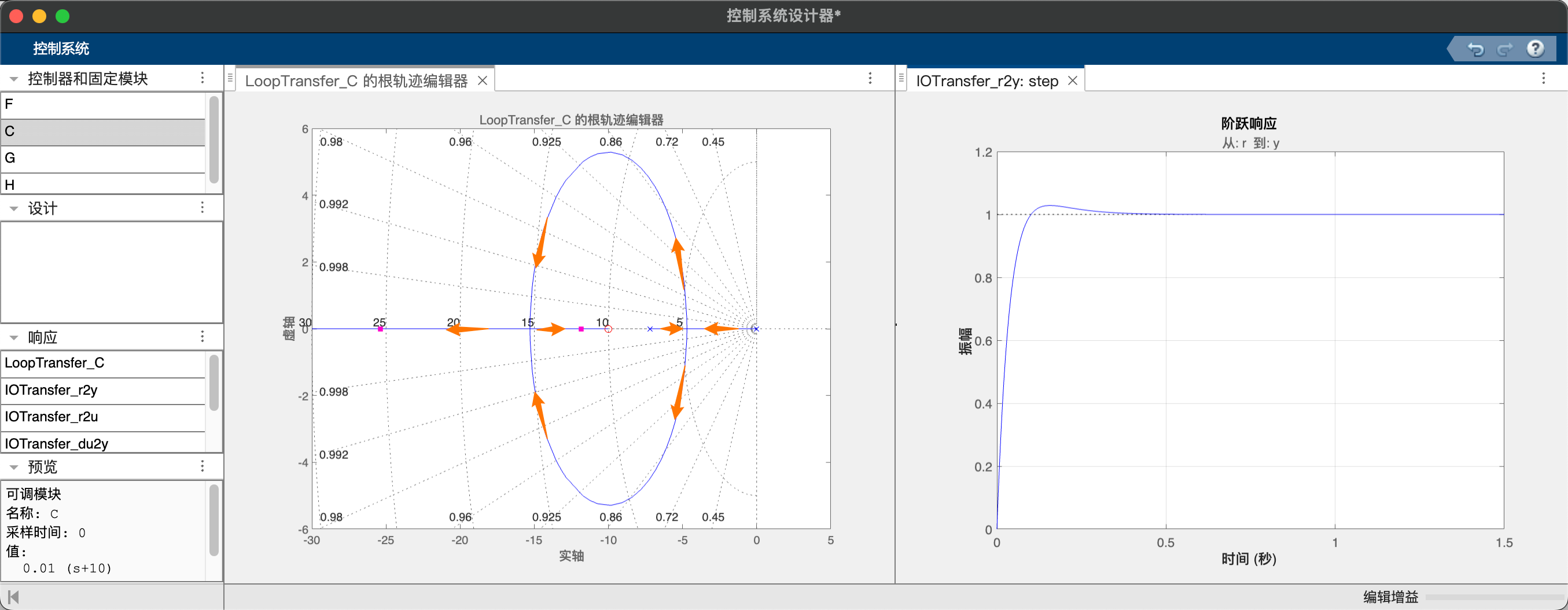
取$-\frac{k_p}{k_d}=-\frac{0.1}{0.01}=-10$，系统的闭环极点可以放置到更远离实轴的地方，阶跃响应有更快的过渡时间和响应超调。

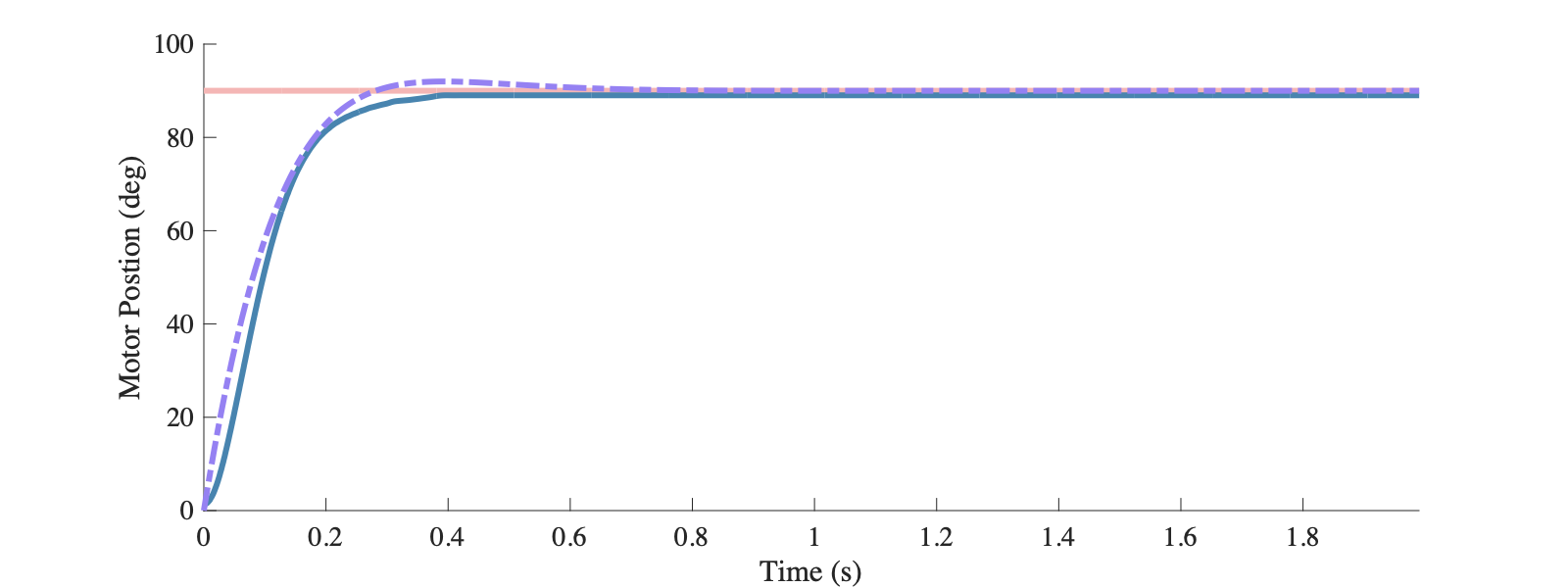
位置控制 - 多环路PID

SISO系统的另一种设计思路是，将系统拆分级联的子系统，再由内而外的分别设计控制器，也就是机电系统常用的多环路控制。考虑到前面我们已经设计好了速度控制器，构建如下的反馈控制框架：

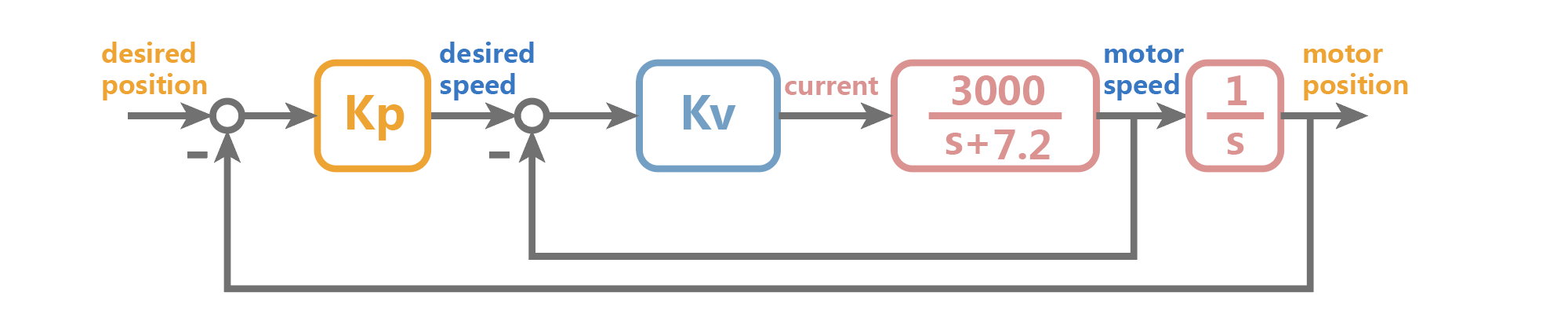
在前面电机角度的比例控制中，位置控制器根据误差产生控制电流，电机电流与角度是二阶关系，因此容易产生震荡和超调；而这里位置控制器根据位置误差产生速度指令，电机转速与角度为一阶关系，作用过程更加直观。一般情况下对于多环路PID，先调节内环系统的控制参数，在调外环，且内环比外环有更快的响应速度。考虑当Kv=0.03时，内环系统的传递函数为：

$\Phi_{inner}(s)=\frac{90}{s+97.2}$

外环系统的传递函数为：

$\Phi_{outer}(s)=\frac{k_p\frac{\Phi_{inner}}{s}}{1+k_p\frac{\Phi_{inner}(s)}{s}}=\frac{90k_p}{s^2+97.2s+90k_p}$

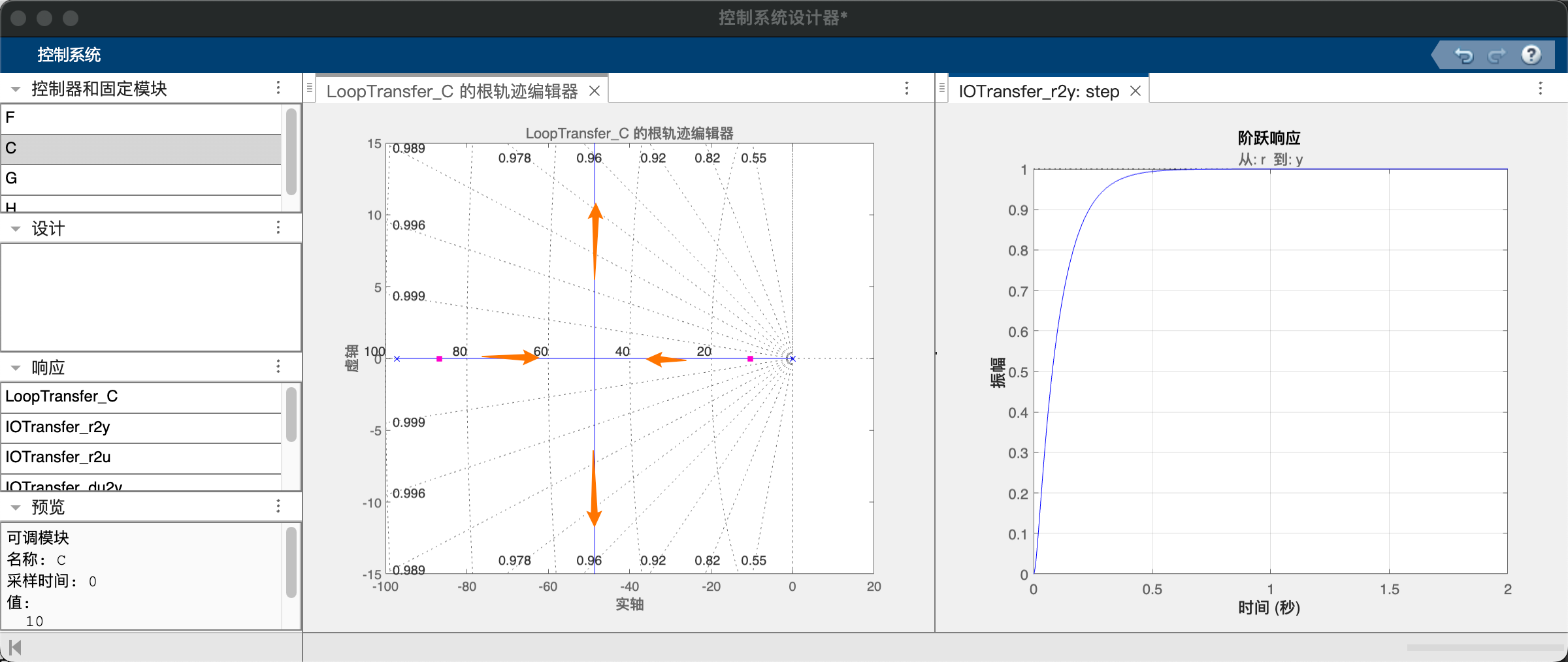
相比于直接的位置比例控制，多环路PID的根轨迹也是在负实轴交汇后发散到无穷远，但由于内环的反馈调节，开环极点被调整到非常远离实轴的位置(-97.2)，系统的响应速度变快。这里设置Kp=10，则位置外环的响应时间为0.39s，速度内环的响应时间为0.04s，相差约十倍。

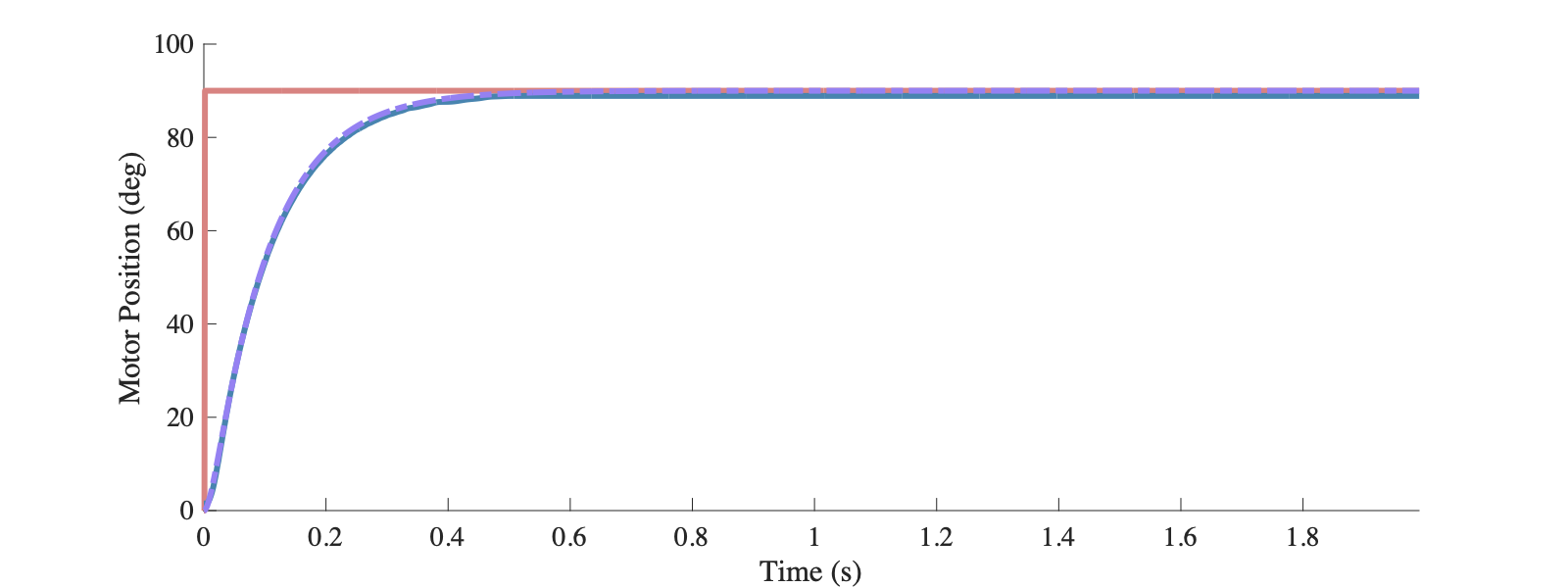
在多环路的控制系统里面我们隐隐约约出现了多个控制目标：电机速度和电机角度。实际上对于经典控制理论来说，我们只能处理SISO系统，多环路控制将每个环路看做一个SISO系统，并将多个系统级联起来。后面一节我们将介绍考虑多状态量的状态空间方法。

Reference

胡寿松.自动控制原理(第四版)[M].科学出版社,2001.
2.