控制系统实践1 - 系统建模与辨识

前言

本教程主要在经典控制、现代控制、非线性控制的基础上，以M3508电机为控制对象（控制器为dSPACE），利用Matlab软件进行控制器设计与分析，并在dSPACE上将算法实现出来，尽可能将理论和实践结合起来，帮助HRIG Lab的小伙伴对控制有一个初步的概念，同时相关公式和算法也方便读者作为实践参考。

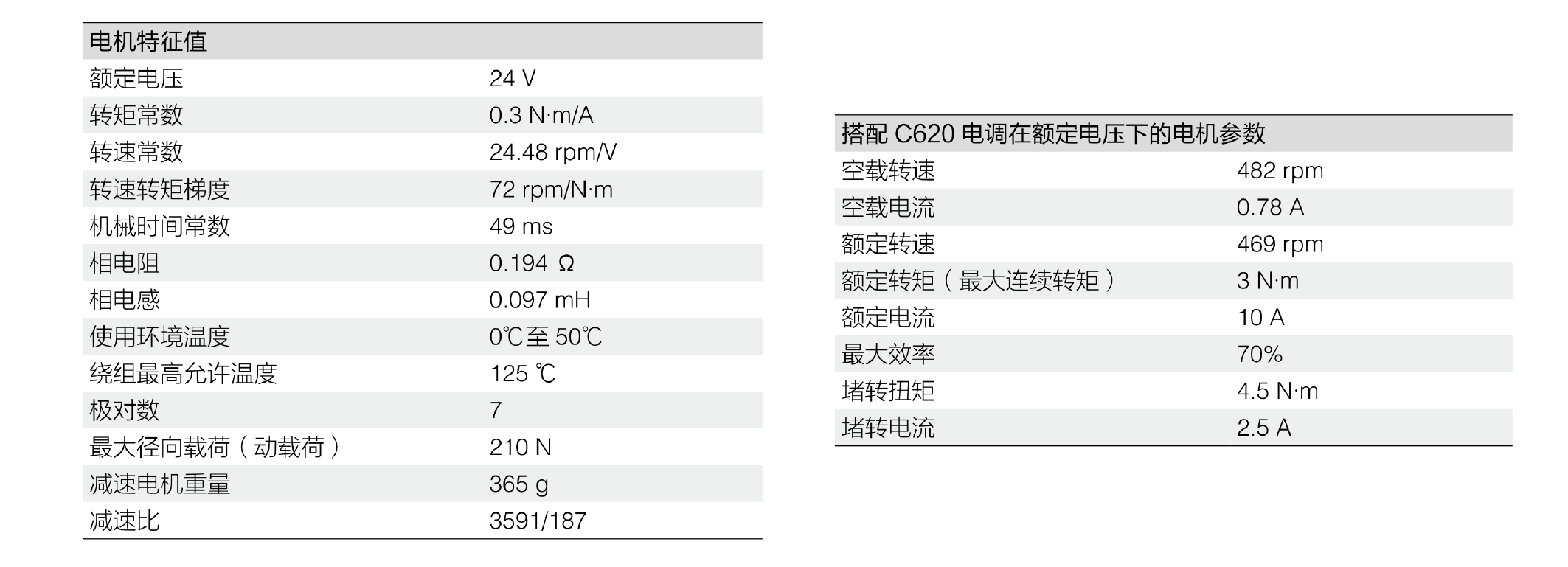
在本系列的教程中，我们的控制对象为大疆RoboMaster比赛专用的M3508电机，使用C620电调驱动，所有算法通过dSPACE控制器在线运行，采样与控制频率均为1KHz，整个系统的硬件结构如下图所示。由于采样频率较高，教程中的部分地方忽略了连续系统与离散系统的差异，使讨论不至于过于复杂。关于dSPACE的使用方法，以及通过CAN总线与M3508电机通信，参考之前的相关教程。

电机的动力学模型推导

为推导电机模型，我们首先推导电机的电流-转速方程：

$J\alpha+K_f\omega=\tau_i,\quad \alpha=\dot\omega,\quad \tau_i=K_i i_a$

其中$J$为电机输出轴的转动惯量，我们在末端安装了一个转盘以增加转动惯量并模拟带负载的情况；$K_f\omega$为齿轮箱的线性摩擦阻力，$\tau_i$为电机的驱动转矩，由驱动电流$i_a$产生，转矩常数$K_i$根据手册参考值为0.3Nm/A。

由此得到电机动力学方程，以及系统的开环传递函数：

$K_m\dot\omega+K_f\omega=K_ii_a$ $G(s)=\frac{w(s)}{i(s)}=\frac{K_i}{K_ms+K_f}=\frac{K_0}{T_ms+1}=\frac{K}{s+\lambda_0}$

传递函数模型的时域辨识

对于一阶系统而言，我们可以根据系统的阶跃响应特性来对系统参数进行辨识。为此我们需要给系统加入阶跃电流输入，并记录电机速度的响应特性。在Simulink中我们可以使用Step模块来生成阶跃输入，但由于噪声与测量误差，往往需要测量同一条件的多次结果，所以更适合使用Pulse Generator模块来生成方波信号。注意实际电机的速度和电流都有饱和特性，因此驱动电流的幅值不应太大。

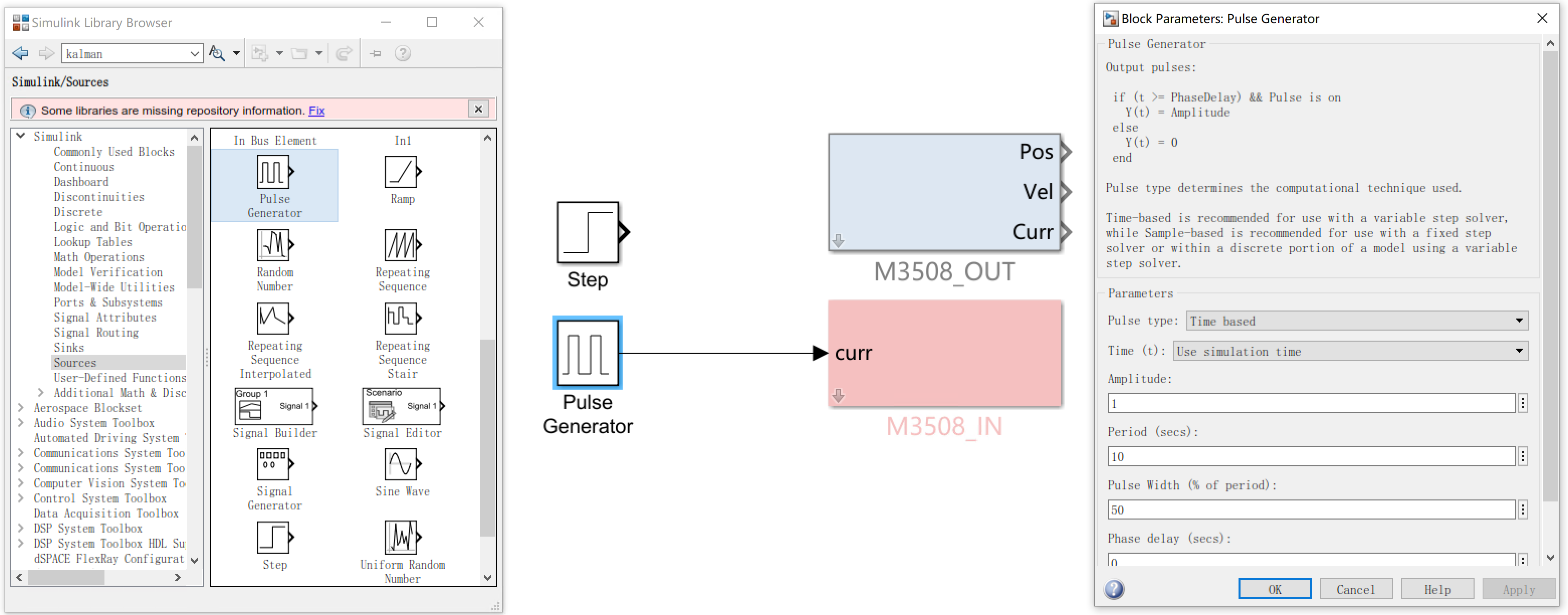
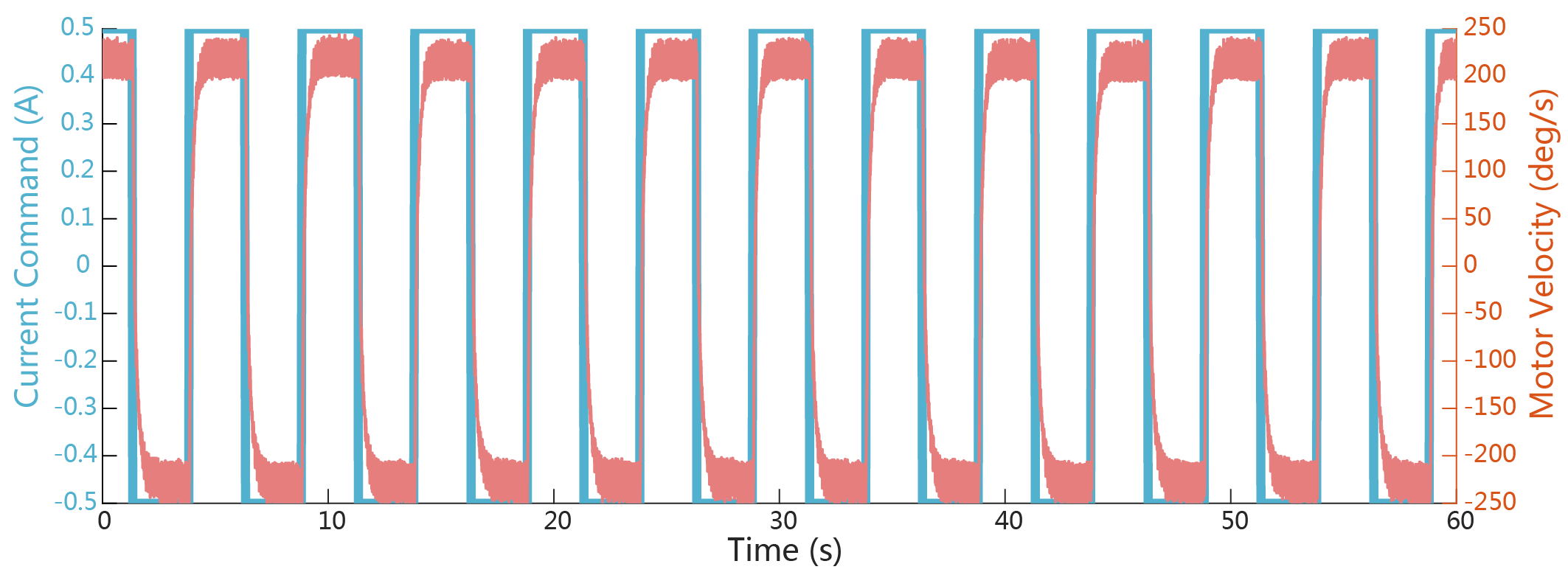
在本次实验中，我们实际施加的驱动电流为$\pm$0.5A的方波信号，电机的转速响应如下，并对多次实验的结果进行平均：

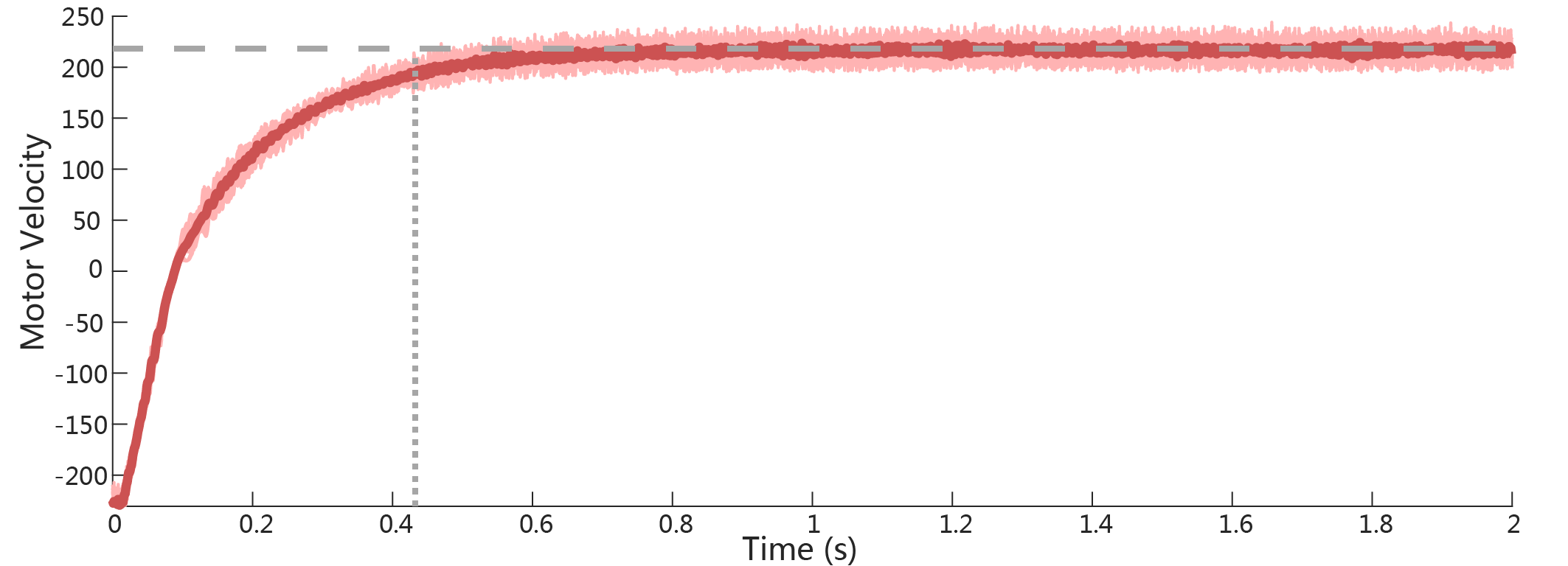
通过观察平均的阶跃响应曲线，可以得到响应的稳态幅值$K_o$约为436 $^\circ \text{s}^{-1}$/A，到达95%稳态的调节时间$T_s$=0.42s，结合传递函数可得：

$K_0=\frac{K_i}{K_f}=436,\quad T_s=3T_m=3\frac{K_m}{Kf}=0.42 \\ \to \quad G(s)= \frac{K_0}{T_ms+1}=\frac{436}{0.14s+1}=\frac{3114}{s+7.14}$

我们可以通过Matlab的系统辨识工具箱来帮助我们得到系统更准确的参数。在App中打开System Identification，选择导入时域数据，将工作区间的变量名填写到输入输出，设定开始时间和采样频率即可。在数据区下方可以选择显示数据的时域或频域，方便确认是否导入正确的数据。

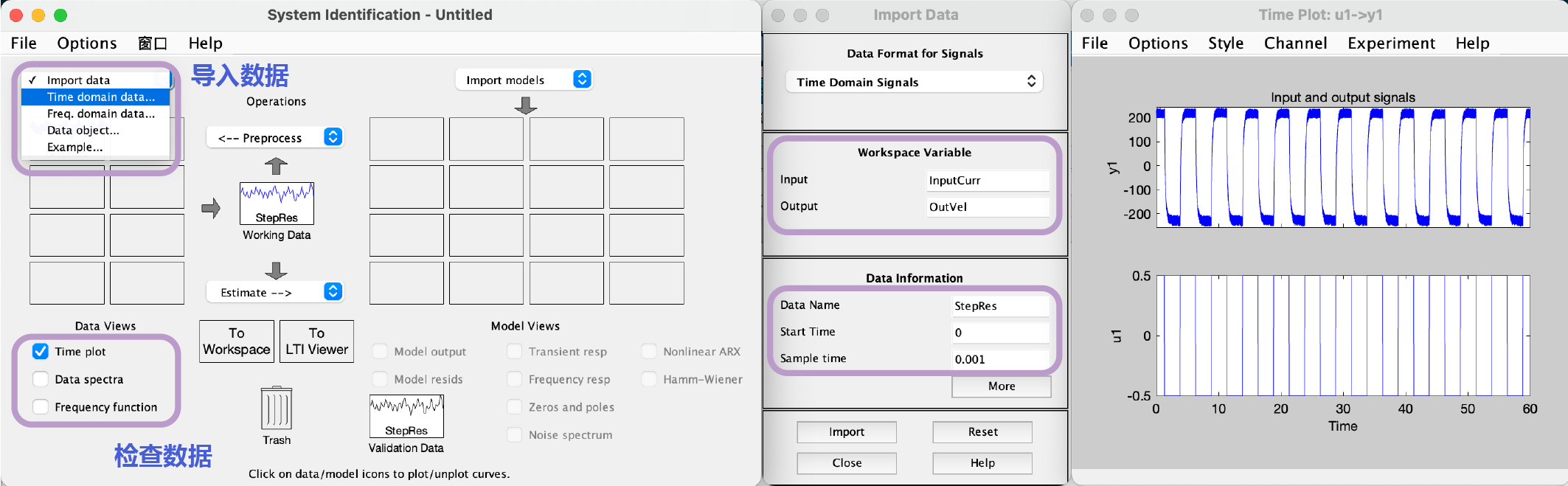
之后我们将数据拖进工作区，选择Estimate Transfer Function Models，并设置便是模型的结构。对于我们的系统来说，只有一个极点。

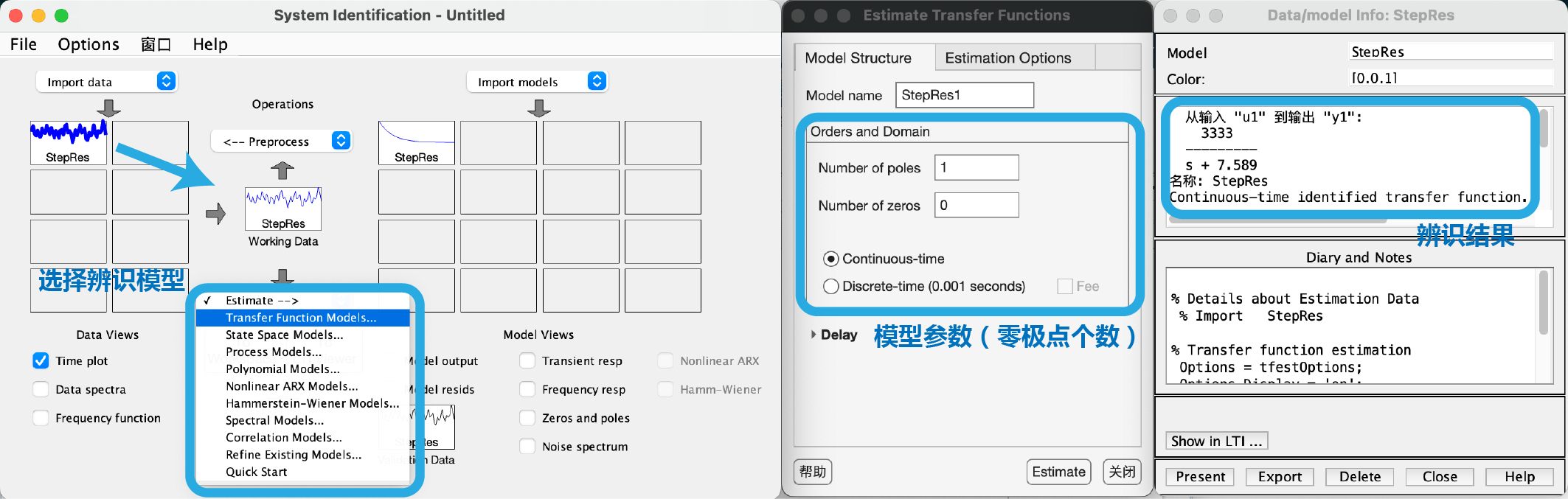
之后点击Estimate即可得到参数估计，Matlab辨识的结果如下，和我们通过观察得到的结果相近。

$G(s)= \frac{3333}{s+7.589}$

传递函数模型的频域辨识

在进行系统辨识时，尤其是较为复杂的系统，为使辨识的结果尽可能准确，输入信号尽可能平均的包含所有频率的成分。阶跃信号虽然也包含全部频率的分量，但主要以低频为主，因此在系统具有高频特性时辨识会不准确。通过系统的频率响应不仅可以帮助我们确定不同频段的参数，还能够帮助我们确定系统的结构。

系统的频率响应曲线可以通过两种方式来实现。第一种是通过扫描的频率输入并记录响应的输出，记录每个测试频率点上的幅值和相角，并连成曲线。例如令$i_a(t)=A_isin(2\pi F t)$，其中F取0.1Hz到50Hz，间隔0.1Hz。在1Hz时的响应如下：

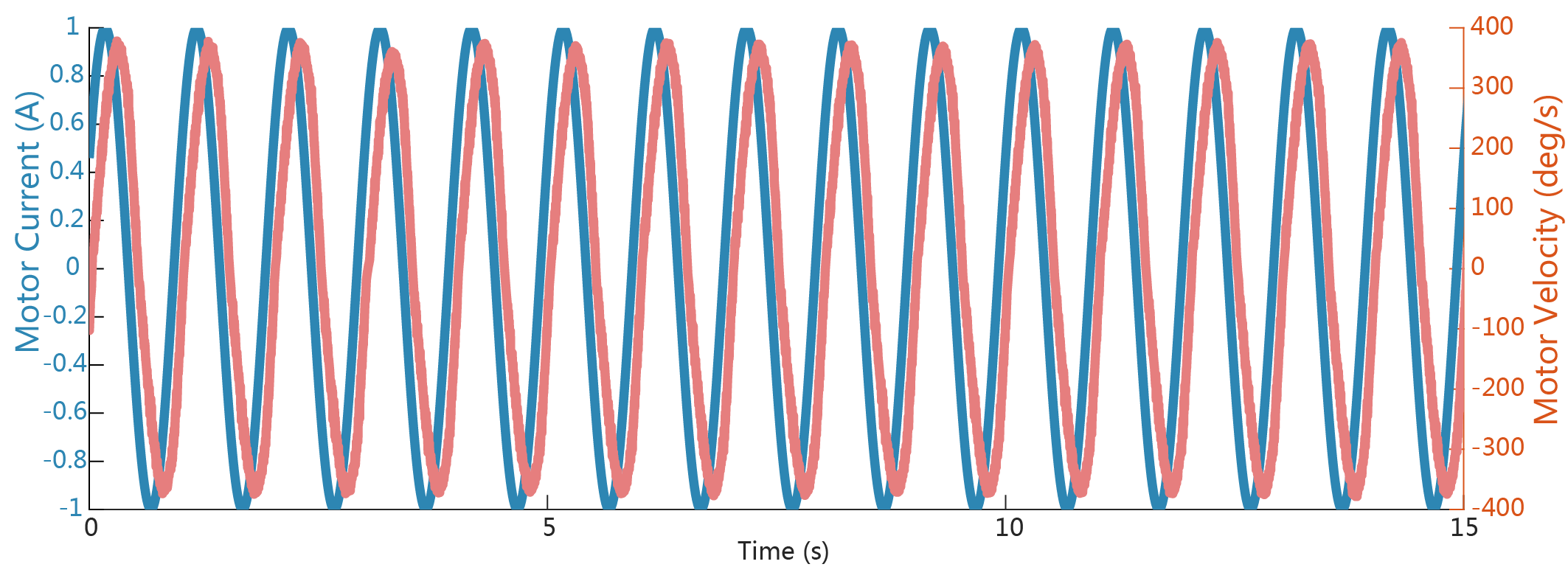
这种扫频试验操作起来费时费力，另一种测量频响方式是让输入信号包含“连续”变化的频率，例如：

$i_a(t)=A_isin(\omega t),\quad\omega=2\pi K_\omega t$

这样正弦信号的频率$\omega$随时间变化，由低频逐渐过渡到高频，通过一次实验即可得到系统的频响（一般也需要多次实验），系统的响应如下：

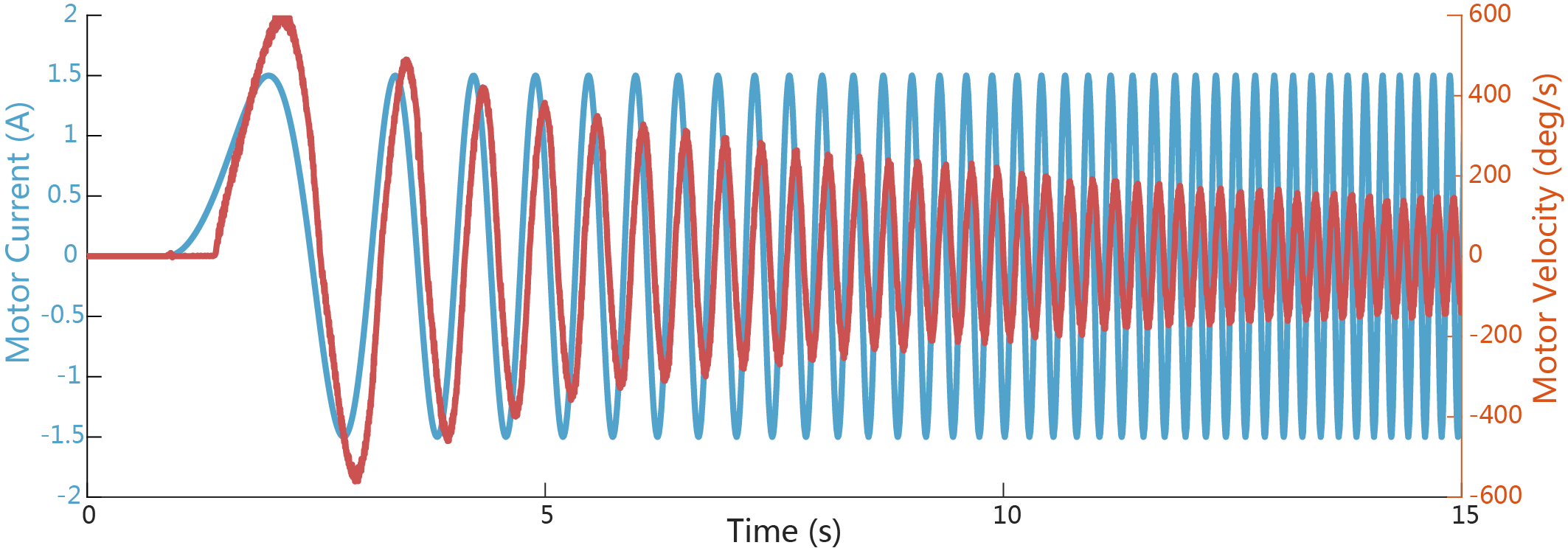
对输入和输出信号进行FFT，可得到幅频响应如下：

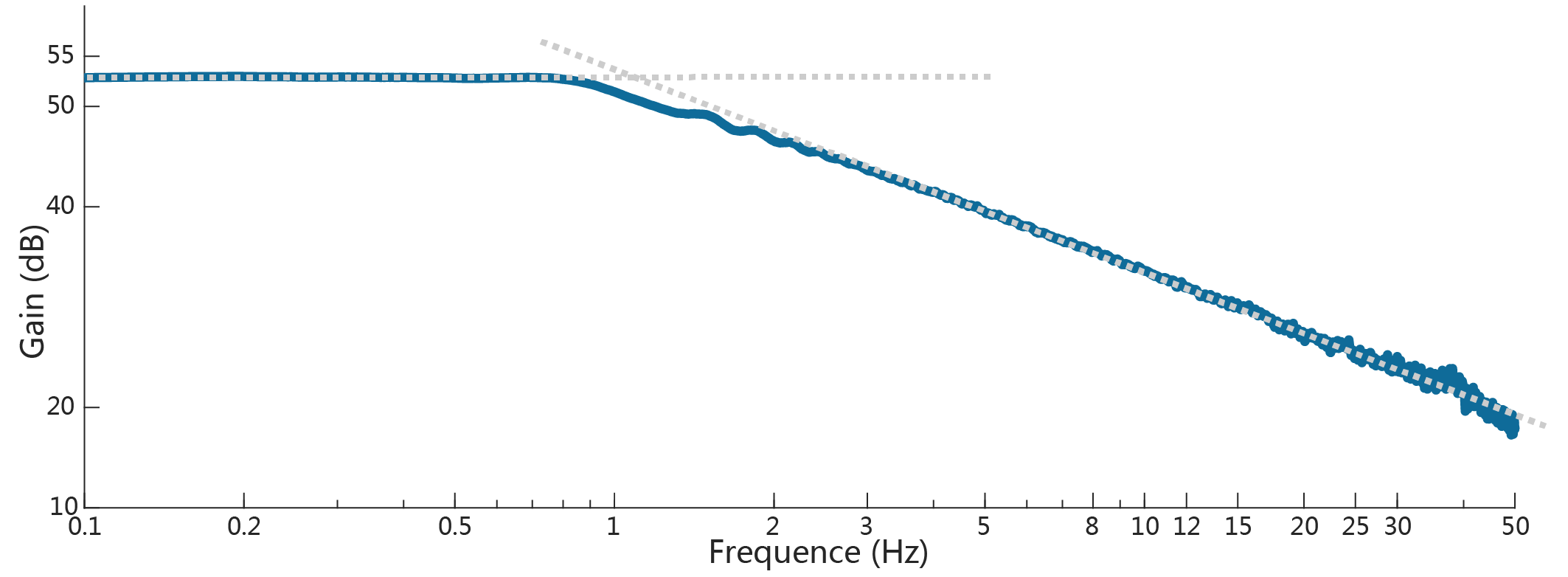
通过观察图像可以得到开环增益为52.8dB，转折频率1.134Hz，由此可得系统模型：

$20log_{10}K_0\ \to\ K_0=436.5\\ \frac{1}{2\pi}\lambda_0=1.134\ \to \ \lambda_0=7.12\\ G(s) = \frac{K_0\lambda_0}{s+\lambda_0}=\frac{3108}{s+7.12}$

频域辨识的结果和时域的结果较为一致。同样我们也可以使用Matlab工具箱在进行系统辨识，辨识的结果如下：

$G(s) = \frac{K_0\lambda_0}{s+\lambda_0}=\frac{2979}{s+7.218}$

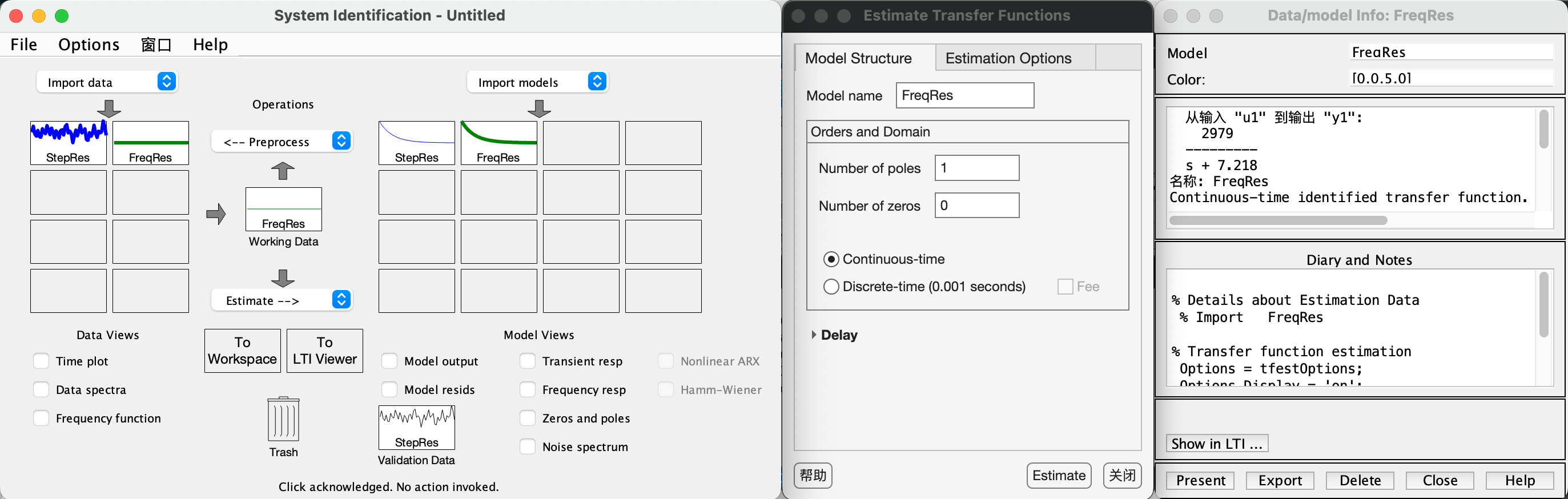
离散系统的辨识

由于控制系统更多运行在计算机中，天然的具有离散系统的性质，因此在主流的系统辨识的教材[1]，大多使用最小二乘方法对系统的离散模型进行辨识。我们控制系统的底层一样是采用离散时间控制，但由于采样频率比较高，因此前面直接估计了连续时间模型，同为也为了后面能够利用经典控制和现代控制来进行控制器的设计和分析，利用连续时间模型能够更简单直观一些。下面我们介绍更为常见的离散系统模型的参数辨识。

考虑一阶SISO系统的有如下的模型：

$w(k+1)=aw(k)+bi_a(k)$

对于一组时间序列的输入输出：$w(1),w(2),\dots,w(n+1);i_a(1),i_a(2),\dots,i_a(n+1)$，构造如下变量：

$\phi_k=[w(k),i_a(k)]^T,\quad\Theta=[a,b]^T\\ \Phi_N=[\phi_1,\phi_2,\dots,\phi_N]^T,\quad Y_N=[w(2),w(3),\dots,w(n+1)]^T$

则有：

$Y_N=\Phi_N\Theta$

推导该方程的最小二乘解：

$\Phi_N^TY_N=\Phi_N^T\Phi_N\Theta \ \Rightarrow\ \Theta=(\Phi_N^T\Phi_N)^{-1}\Phi_N^TY_N$

Matlab中在频率响应数据的基础上，通过以下代码的到模型的参数：

len = 60000;
Phi=[OutVel(1:len-1),InputCurr(1:len-1)];
Y = OutVel(2:len);
Theta = inv(Phi'*Phi)*Phi'*Y;

$w(k+1)=0.9939w(k)+2.9697i_a(k)$

考虑前面已经辨识得到系统的传递函数模型，选定近似参数如下：

$G(s) = \frac{3000}{s+7.2}$

在Matlab中通过以下代码可将连续系统模型转换为离散模型：

1 2	Model_C = tf([3000],[1 7.2]); Model_D = c2d(Model_C, 0.001); % Ts = 0.001

$G_d(z) = \frac{2.989}{z-0.9928}$

或者在Matlab辨识工具箱中选择辨识离散模型：

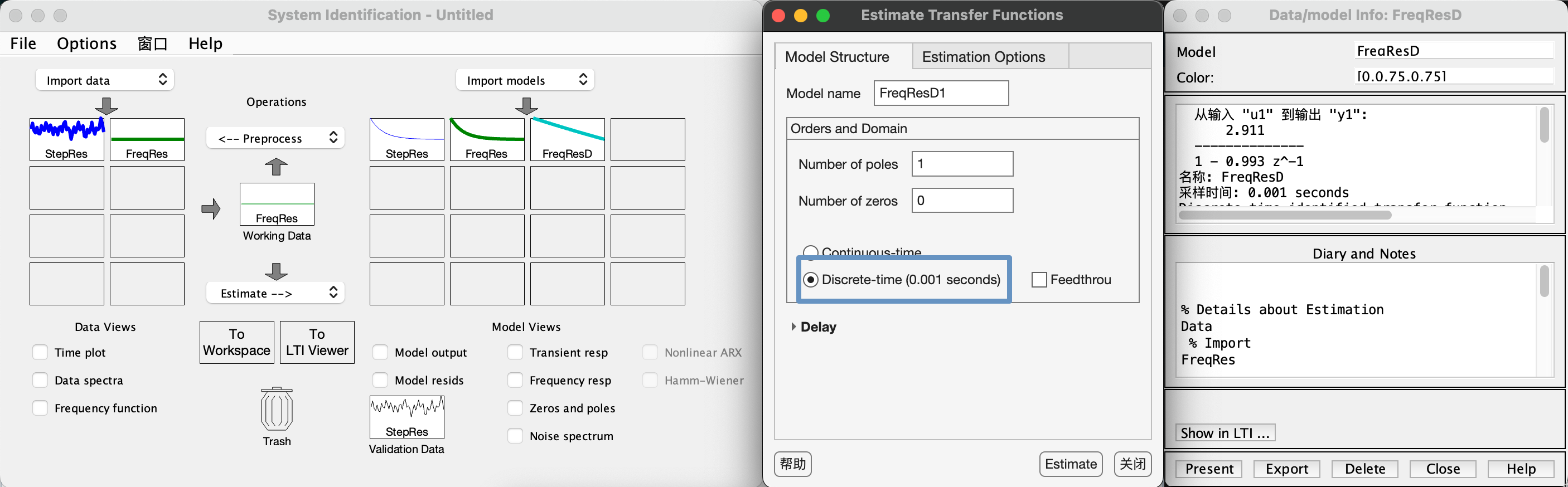
模型辨识的不准确性

可以看出，通过不同的实验和不同方法得到的系统模型均存在一定差异。实际上，辨识的结果取决于系统的结构特性、输入信号的分布等多方面的原因。举例来说，在构建动力学模型时，我们认定电机转速和电机电流具有一阶响应关系，然而当我们绘制系统的相频响应（如下图），会发现开环系统存在至少三个极点，因为每个极点会使相位滞后90度，而相位在50Hz时已经超过了-180度。

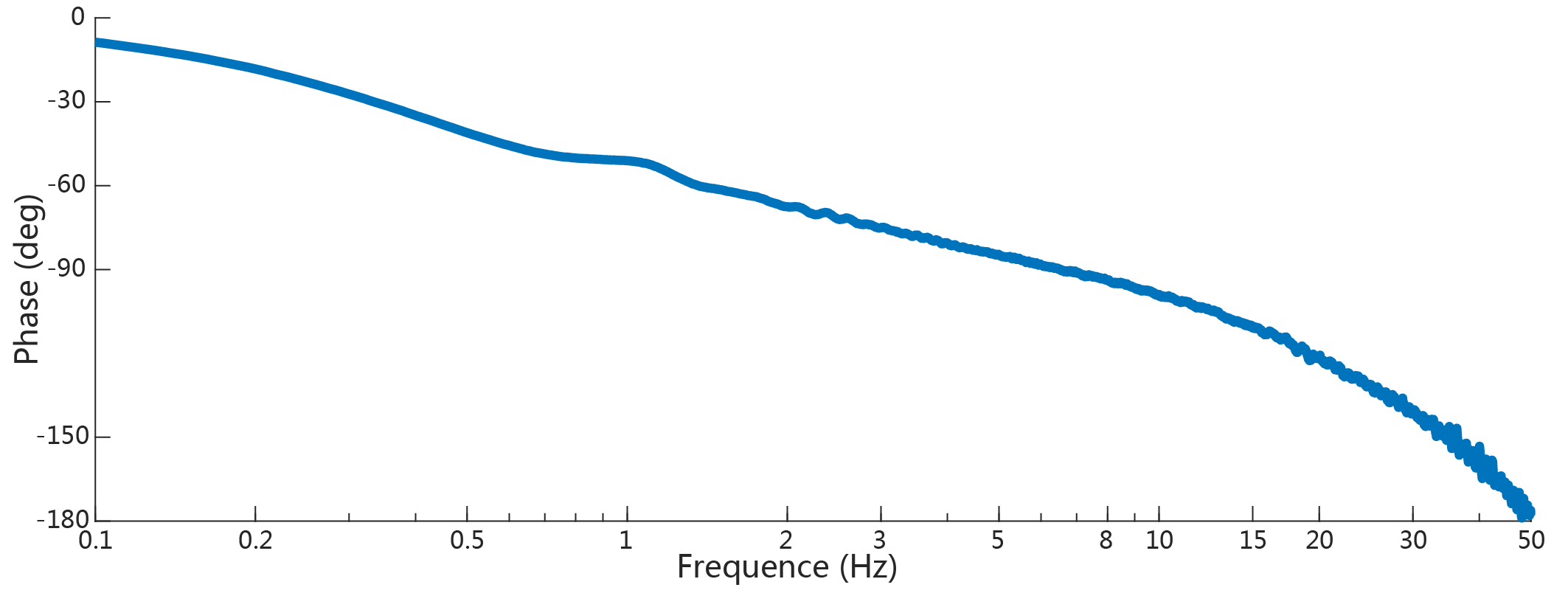
当我们辨识三个极点时，模型具有更高的准确度。如下图所示，通过辨识工具箱得到系统的三个极点分别为$p_1=-4.66,\ p_{2,3}=-212\pm279j$，其中$p_{2,3}$极点的实部远小于$p_1$极点，整个系统的响应由$p_1$极点主导，而在高频信号输入时，一阶模型将大大失真。

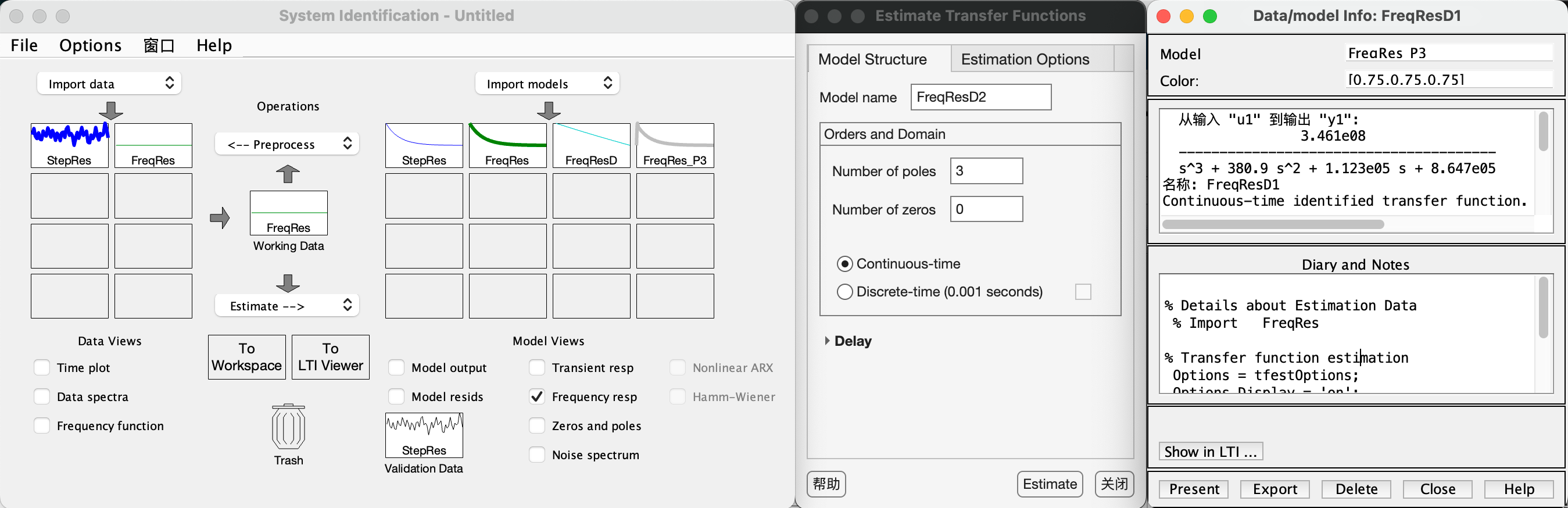
越高阶的模型越难以分析和设计控制器，实现起来也存在更多困难。在实践中，几乎不可能做到完全准确的建模，因此只能将主要分析和关注的系统特性描述出来，并尽可能降低模型复杂度。为简单起见，本教程的余下部分均采用一阶模型，且选定模型如下：

$G(s) = \frac{3000}{s+7.2}$ $G_d(z) = \frac{2.989}{z-0.9928}$

Reference

胡寿松.自动控制原理(第四版)[M].科学出版社,2001.
刘金琨,沈晓蓉,赵龙.系统辨识理论及MATLAB仿真[M].电子工业出版社,2013.