将一个复杂的问题,转化为可以递归的子问题,尽可能减少解的可能空间,然后进行局部暴力破解。
DP的特性与步骤(SRTBOT)
- 定义子问题(subproblem)
- 使用词汇语句来描述子问题
- 通常采用输入的子集:前缀、后缀、子串
- 通常会采用额外的辅助变量对子问题进行扩充
- 关联性(Relate)
- 子问题的求解通过递归来实现,$x(i)=f(x(j),\ \dots)$
- 拓扑顺序(Topological Order)
- 问题的求解时单向递进的,不存在循环的回路
- 基本案列(Basic Cases)
- 不存在关联性的初始状态的解
- 原始问题(Original Problem)
- 展示如何由子问题求解原始问题
时间分析(Time Analysis)
求解原始问题所需求解的所有子问题时间总和
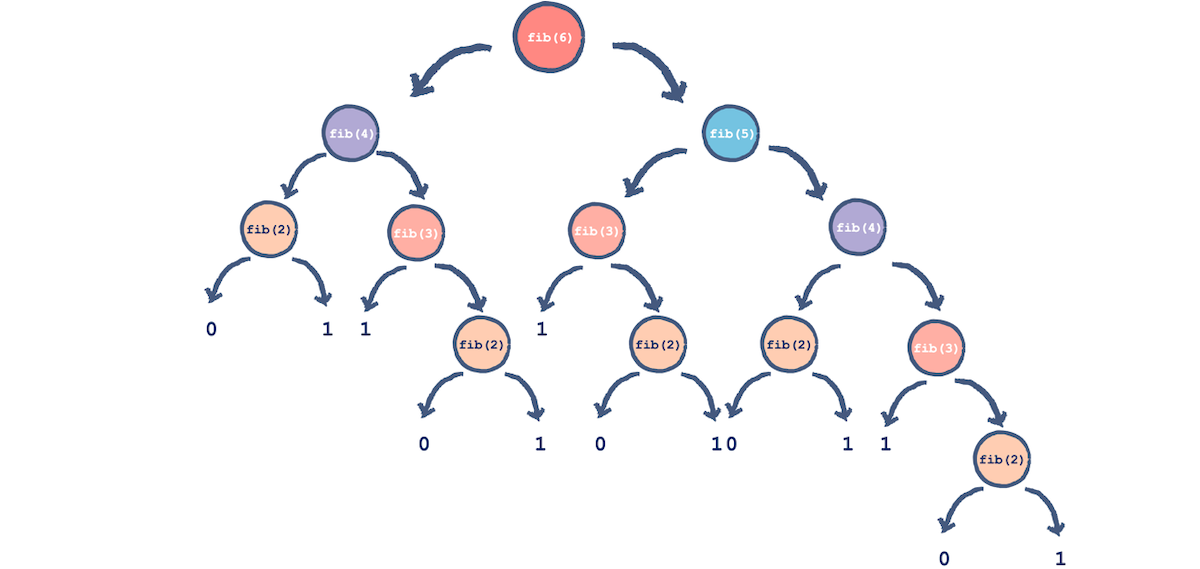
Trick 1: 增加记忆 - 斐波那契数
问题:计算第n个斐波那契数$F_n$
DP求解:
- 子问题:计算第i个斐波那契数$F(i),\ i\in\{1, 2, \dots, n\}$
- 关联性:$F(i)=F(i-1)+F(i-2)$
- 拓扑顺序:递增 i
- 基本案例:$F(0)=0,\ F(1)=1$
- 原始问题:$F_n = F(n)$
- 时间分析:
1 | def fib(n): |
Trick 2: 局部暴力破解 - 保龄球问题
问题:在一组给定带标签的保龄球数列,计算最大得分
- 每次可以击中一个或相邻两个保龄球,也可以选择不击球(结束)
- 击中一个得该球分数,击中相邻讲个得两球得分乘积
- 测试案例:$[-1,1,1,1,9,9,3,-3,-5,2,2]$
DP求解:
- 子问题:求解输入的子序列的最大得分
B(i) = Max Score of Input v[i:n] - 关联性(局部暴力破解):
B(i) = max{B(i+1), B(i+1)+v[i], B(i+2)+v[i]*v[i+1]} - 拓扑顺序:递减 i
(for i = n, n-1, 0) - 基本案例:
B(n) = B(n+1) = 0 - 原始问题:
B(0) - 时间分析:
Time = O(n) subproblems * O(1) work on each = O(n)
1 | def bowl(v): |
Trick 3: 通过子序列构造子问题 - 最长相同子序列(Longest Common Subsequence, LCS)
问题:给定两个字符串,找出两个字符串最长的公共部分
- 测试案例:
A = hieroglyphology, B = michaelangelo - 解集:
hello, heglo, iello, ieglo
DP求解:
- 子问题:
x(i,j) = Longest Common Subsequence of A[i:n] and B[j:n] - 关联性(局部暴力破解):
- 拓扑顺序:递减 i + j;先递减 i,然后递减 j
- 基本案例:
x(i,|B|) = x(|A|,j) = 0 - 原始问题:
x(0,0) - 时间分析:
Time = O(|A|+1)*O(|B|+1) subproblems * O(1) work on each = O(|A|*|B|)
1 | def lcs(A, B): |
Trick 4: 增加问题约束 - 最长递增子序列(Longest Increasing Subsequence, LIS)
问题:给定一个字符串,找出最长的严格递增的子串
- 测试案例:
A = carbohydrate - 解集:
abort
DP求解:
- 子问题:包含首个元素的最长递增子序列
x(i) = Longest Increasing Subsequence of A[i:n] that include A[i] - 关联性(局部暴力破解):
- 拓扑顺序:递减 i
- 基本案例:
x(n) = 1 - 原始问题:
max(x(i)| 0 <= i <= |A|) - 时间分析:
Time = O(|A|) subproblems * O(log|A|) each by AVL Tree = O(|A|log|A|)
1 | def lis(A): |
Trick 5: 子问题扩张 - 括号化算数运算(Arithmetic Parenthesization)
问题:给定一个算数表达式$a_0 _1 a_1 _2 a_2 \cdots *_{n-1} a_{n-1}$,通过添加括号使运算结果最大化
- $*_i \in\{+, \times\}$,$a_i$为正、负整数
- 测试案例:$7+(-4) \times 3+(-5)$
- 解集:$((7)+((-4) \times((3)+(-5))))=15$
DP求解:
- 子问题:求解输入的子序列的最大和最小运算结果
x(i,j,opt) = opt value of subsquence$a_i_{i+1}\cdots_{j-1}a_{j-1}$0 ≤ i < j ≤ n, opt in {max, min}
- 关联性(局部暴力破解):
- 拓扑顺序:递增 j - i
- 基本案例:
x(i,i+1,opt) = A[i] - 原始问题:
x(0,n,max) - 时间分析:
Time = O(n^2) subproblems * O(n) work on each = O(n^3)
1 | def ap(A, O): |