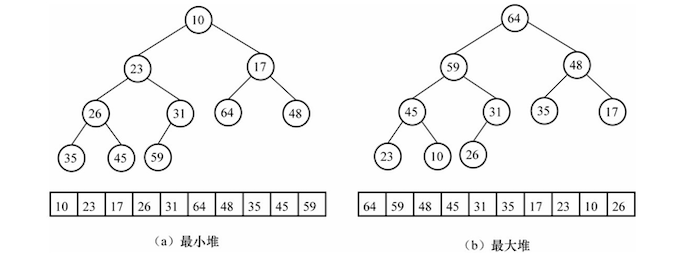
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| class PriorityQueue:
def __init__(self, A):
self.A = []
self.n = 0
def insert(self, x):
self.A.append(x)
self.n += 1
def delete_max(self):
if len(self.A) < 1:
return False
self.n -= 1
return self.A.pop()
@classmethod
def sort(Queue, A):
pq = Queue(A)
for x in A:
pq.insert(x)
out = [pq.delete_max() for _ in A]
out.reverse()
return out
class PQ_Heap(PriorityQueue):
def insert(self, *args):
super().insert(*args)
n, A = self.n, self.A
self.max_heapify_up(A, n, n-1)
def delete_max(self):
n, A = self.n, self.A
A[0], A[n-1] = A[n-1], A[0]
self.max_heapify_down(A, n-1, 0)
return super().delete_max()
def parent(self, i):
p = (i - 1) // 2
return p if 0 < i else i
def left(self, i, n):
l = 2 * i + 1
return l if l < n else i
def right(self, i, n):
r = 2 * i + 2
return r if r < n else i
def max_heapify_up(self, A, n, c):
p = self.parent(c)
if A[p].key < A[c].key:
A[c], A[p] = A[p], A[c]
self.max_heapify_up(A, n, p)
def max_heapify_down(self, A, n, p):
l, r = self.left(p, n), self.right(p, n)
if A[r].key < A[l].key:
c = l
else:
c = r
if A[p].key < A[c].key:
A[c], A[p] = A[p], A[c]
self.max_heapify_down(A, n, c)
|