萤火

有一份热，发一分光

0%

算法基础 3 - 排序 Sorting

发表于 更新于 分类于 阅读次数： Valine：

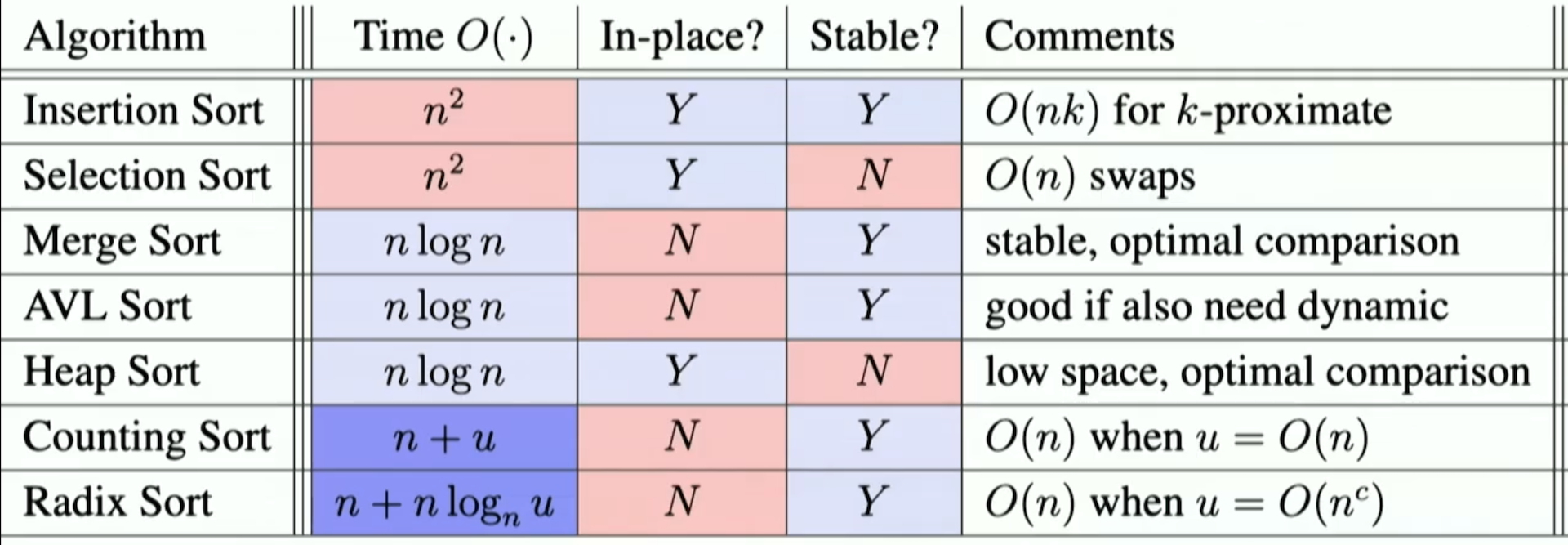
排序算法对比

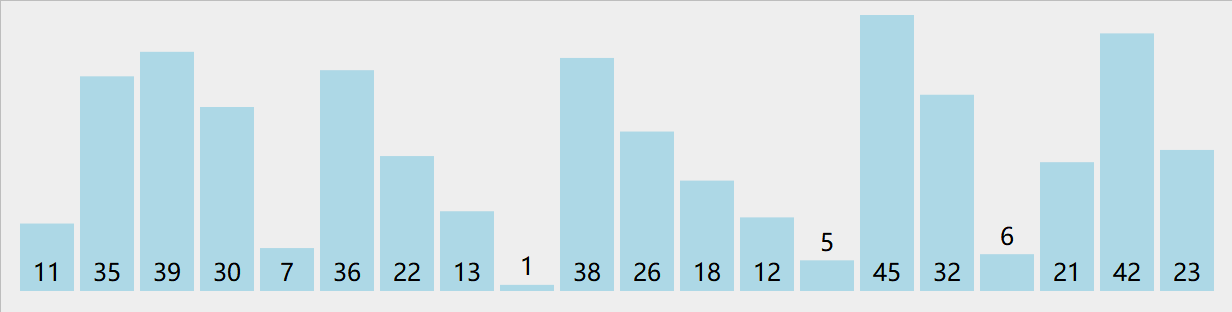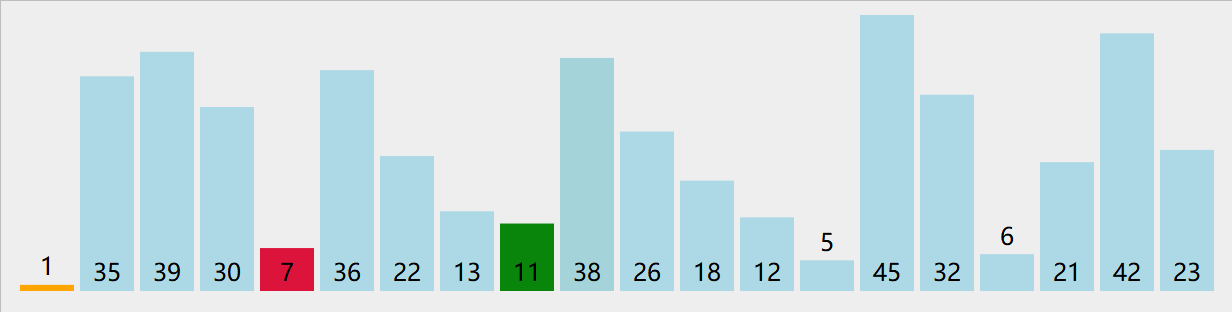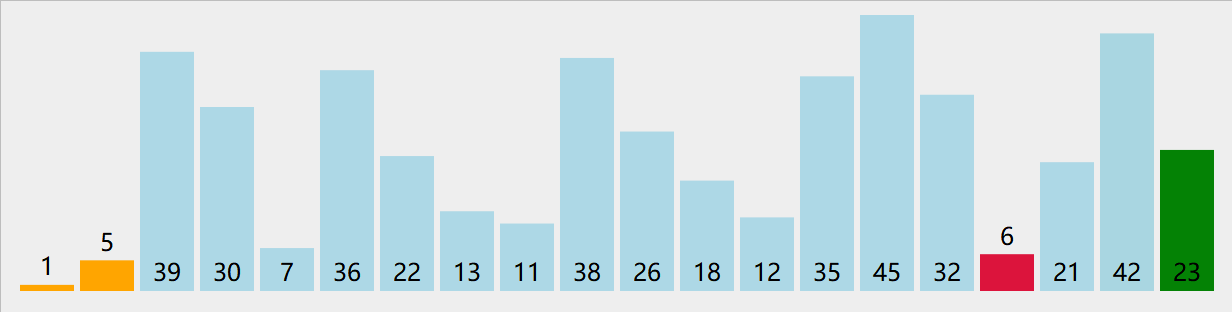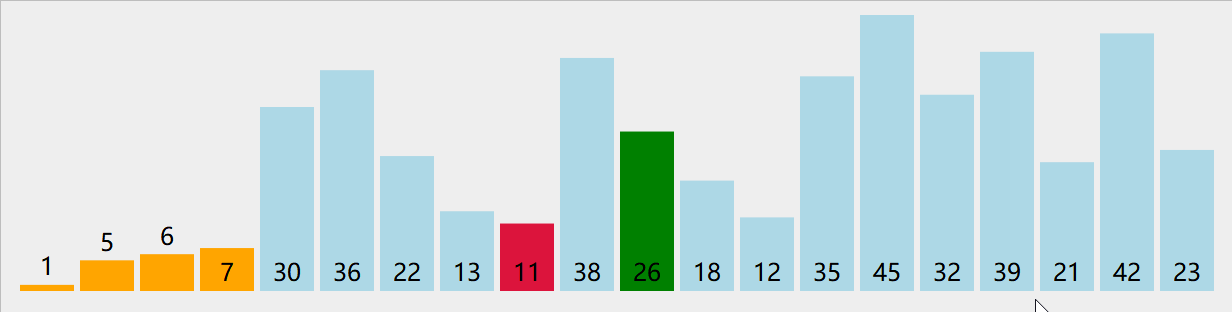
选择排序

  • 每次将未排序序列的最大元素放入已排序序列的开头
  • in-place算法，时间复杂度O(n^2)，排序算法不稳定
1
2
3
4
5
6
7
def selection_sort(A):
    for i in range(len(A)-1, 0, -1):
        m = i
        for j in range(i):
            if A[j] > A[m]:
                m = j
        A[i], A[m] = A[m], A[i]

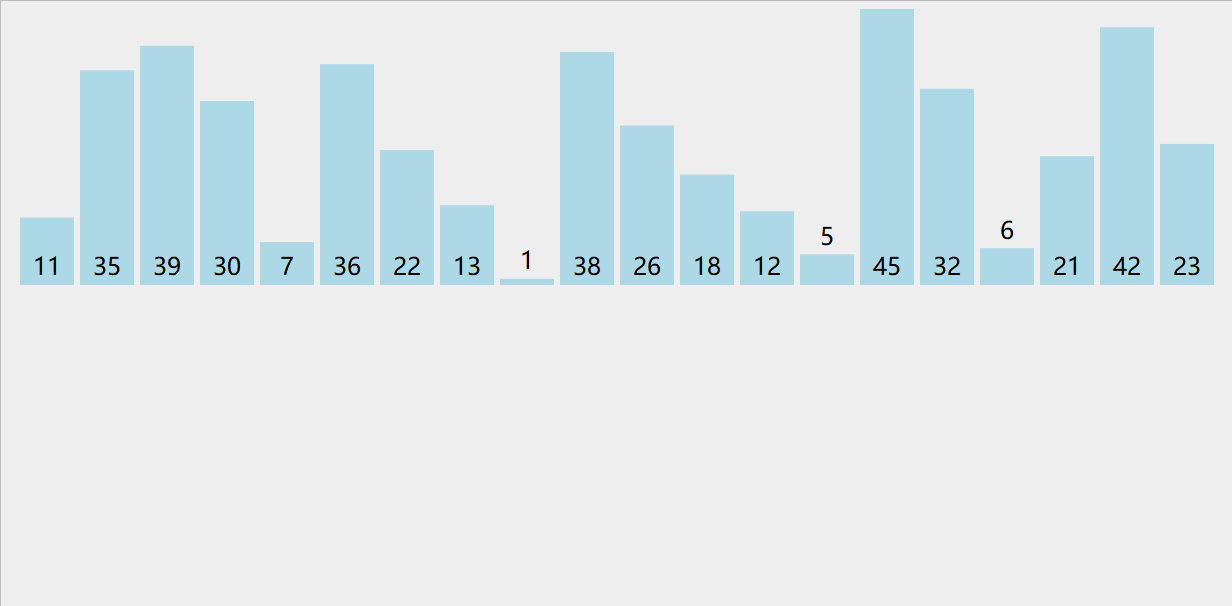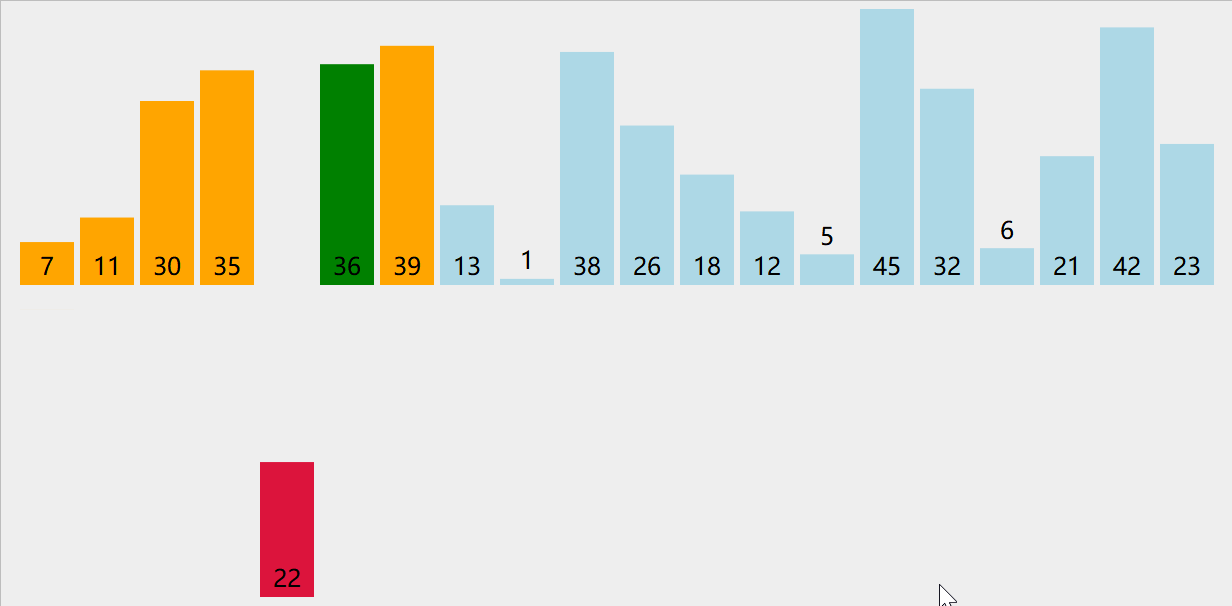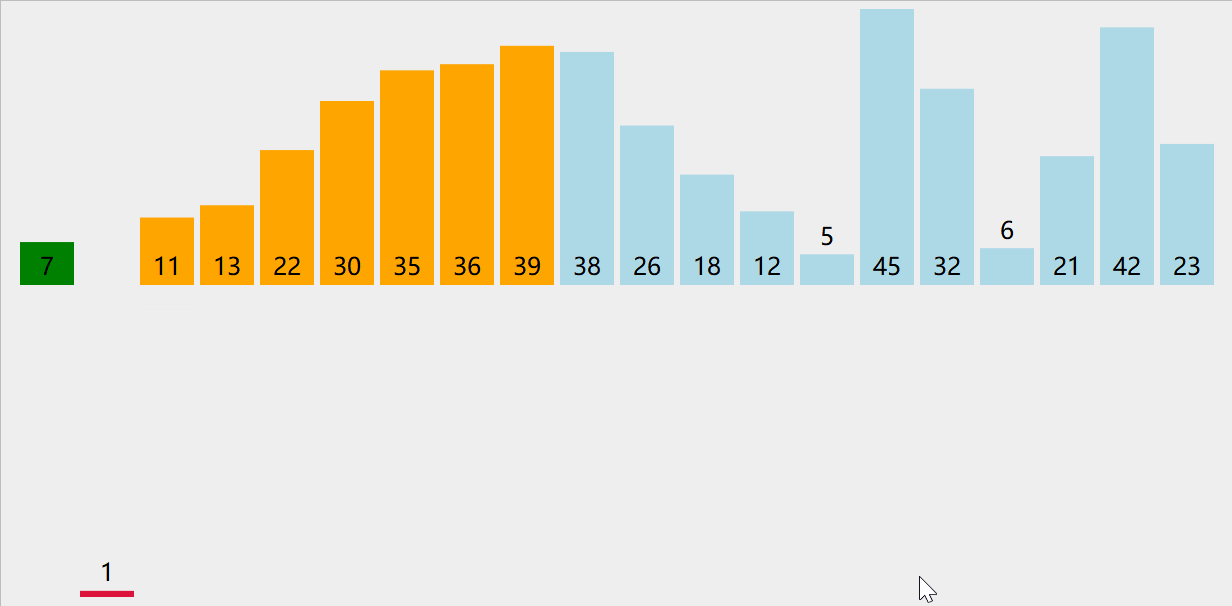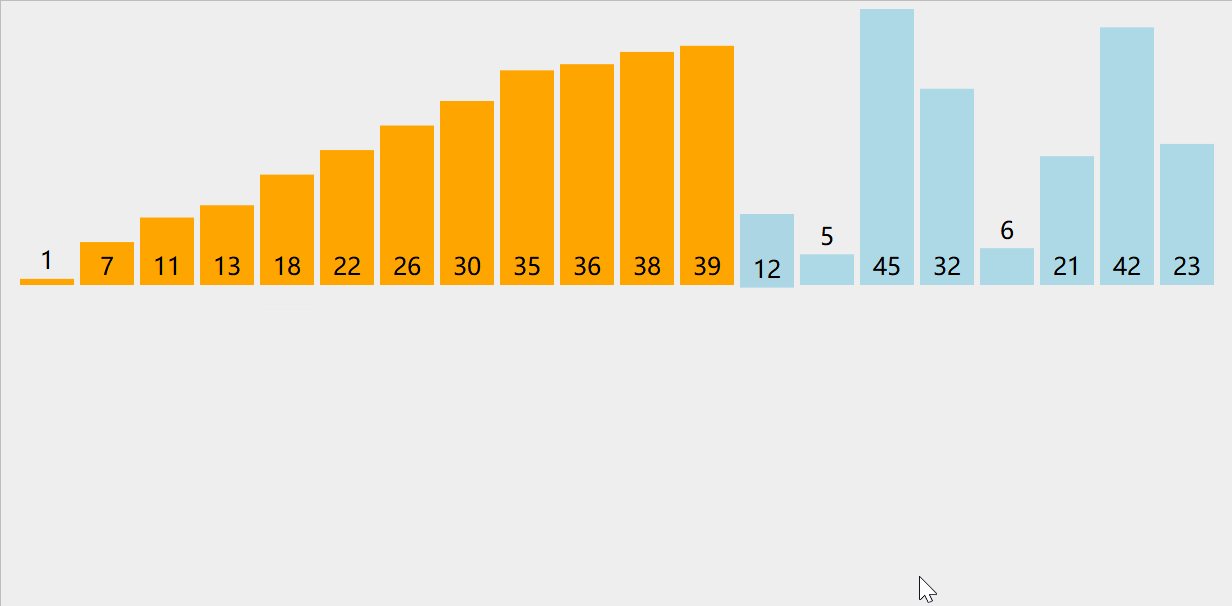
插入排序（Insertion Sort）

  • 每次将一个待排序元素插入到已排序序列中的合适位置
  • in-place算法，时间复杂度O(n^2)，排序算法稳定
1
2
3
4
5
6
def insertion_sort(A):
    for i in range(1, len(A)):
        j = i
        while j > 0 and A[j] < A[j-1]:
            A[j], A[j-1] = A[j-1], A[j]
            j -= 1

冒泡排序（Bubble Sort）

  • 每次交换相邻的两个元素，直至没有需要交换的元素
  • in-place算法，时间复杂度O(n^2)，排序算法稳定
1
2
3
4
5
6
7
8
9
def bubble_sort(A):
    for i in range(len(A)-1, 0, -1):
        exchange = False
        for j in range(0, i):
            if A[j] > A[j+1]:
                A[j], A[j+1] = A[j+1], A[j]
                exchange = True
        if not exchange:
            break

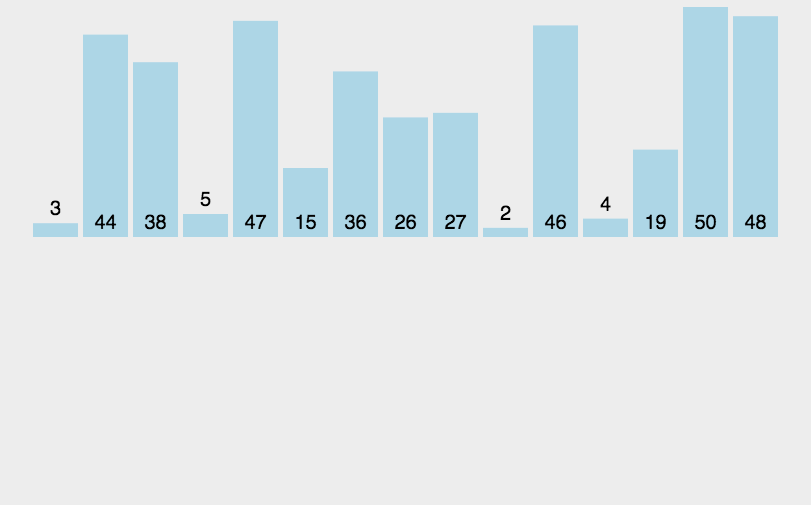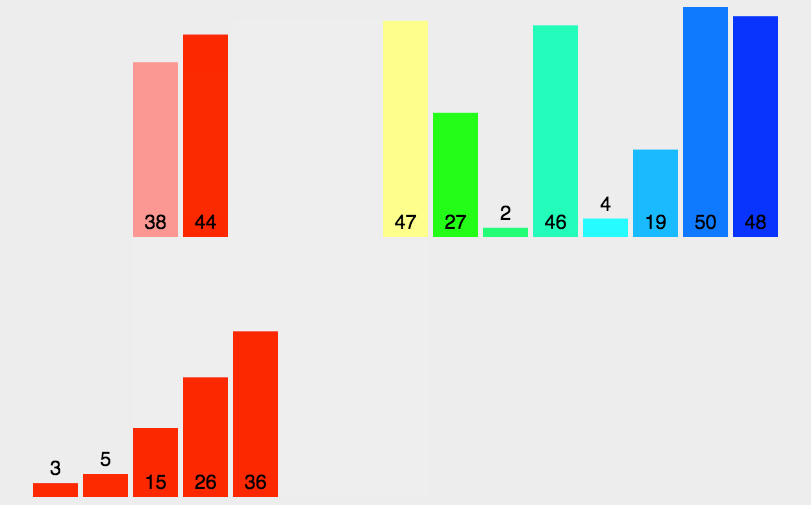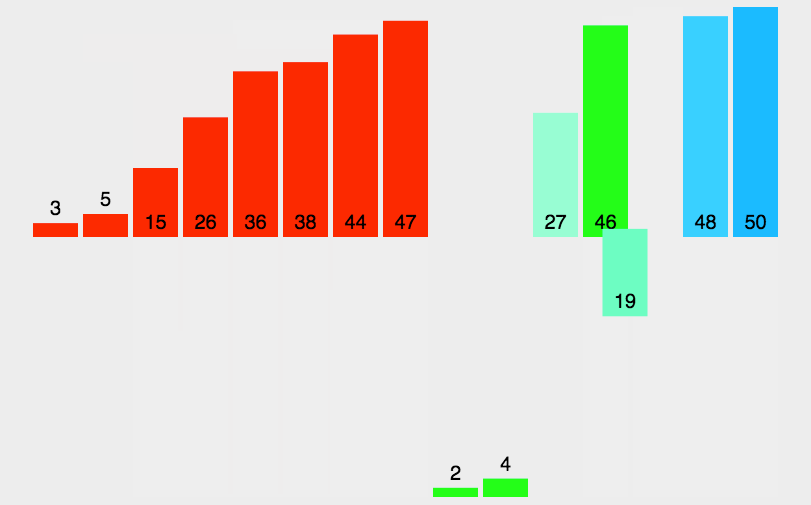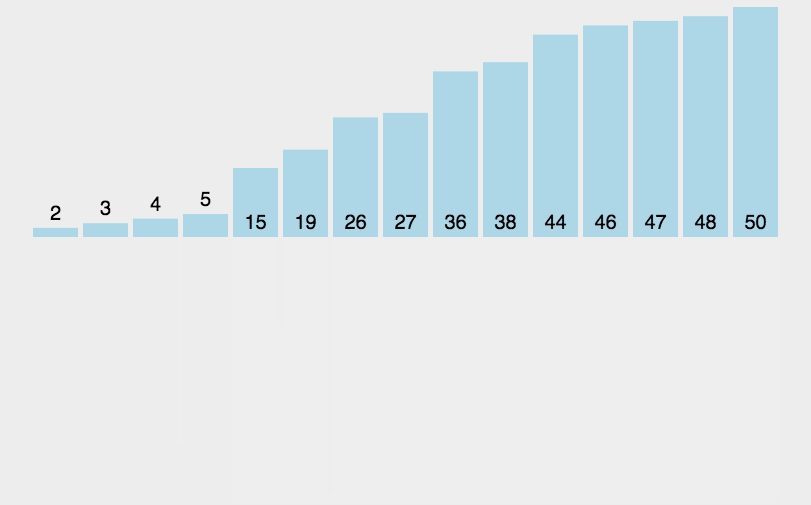
归并排序（Merge Sort）

  • 把一个序列分成两半，先分别对每个子序列排序，然后再将两个子序列合并
  • 一般采用递归法，时间复杂度为O(nlogn)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def merge_sort(A, a=0, b=None):
    if b is None:
        b = len(A)
    if 1 < b - a:
        c = (a + b + 1)//2
        merge_sort(A, a, c)
        merge_sort(A, c, b)
        L, R = A[a:c], A[c:b]
        i, j, k = 0, 0, a
        while k < b:
            if (j >= len(R)) or (i < len(L) and L[i] < R[j]):
                A[k] = L[i]
                i += 1
            else:
                A[k] = R[j]
                j += 1
            k += 1

基数排序（Radix Sort）

  • 在Direct Access Array Sort、Counting Sort、Tuple Sort基础上演化出来的排序算法，将每个整数分解为n的幂次，根据幂级顺序进行元组排序，可以做到线性时间内完成排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
def counting_sort(A):
    "Sort A assuming items non-negative keys"
    u = 1 + max([x.key for x in A])
    D = [0] * u
    for x in A:
        D[x.key] += 1
    for k in range(1, u):
        D[k] += D[k-1]
    for x in list(reversed(A)):
        A[D[x.key] - 1] = x
        D[x.key] -= 1

def radix_sort(A):
    "Sort A assuming items have non-negative keys"
    n = len(A)
    u = 1 + max([x for x in A])
    c = 1 + (u.bit_length()) // n.bit_length()

    class Obj:
        pass

    D = [Obj() for a in A]
    for i in range(n):
        D[i].digits = []
        D[i].item = A[i]
        high = A[i]
        for j in range(c):
            high, low = divmod(high, n)
            D[i].digits.append(low)
    for i in range(c):
        for j in range(n):
            D[j].key = D[j].digits[i]
        counting_sort(D)
    for i in range(n):
        A[i] = D[i].item