萤火

有一份热，发一分光

0%

An Introduction for IMU 2 - IMU数据融合与姿态解算

发表于 更新于 分类于 阅读次数： Valine：

在上一篇博客中，我们已经介绍了IMU的内部工作原理，以及如何通过Arduino读取MPU6050的数据。虽然可以从DMP直接读取姿态角，但其数据返回的频率相对较低，同时由于DMP库不是开源的，其内部的工作原理、输出姿态角的准确性都不清楚；而除了MPU以外的IMU传感器基本不带有DMP功能，因此大部分时候还是需要我们自己在单片机里实现IMU姿态角的计算。本片博客将介绍如何使用采集到的加速度和角速度数据进行数据融合，也就是IMU的姿态解算。

IMU姿态解算

MPU6050得到的原始数据仅有加速度与角速度，单独由加速度计或陀螺仪都可以解算出三轴的角度。

1

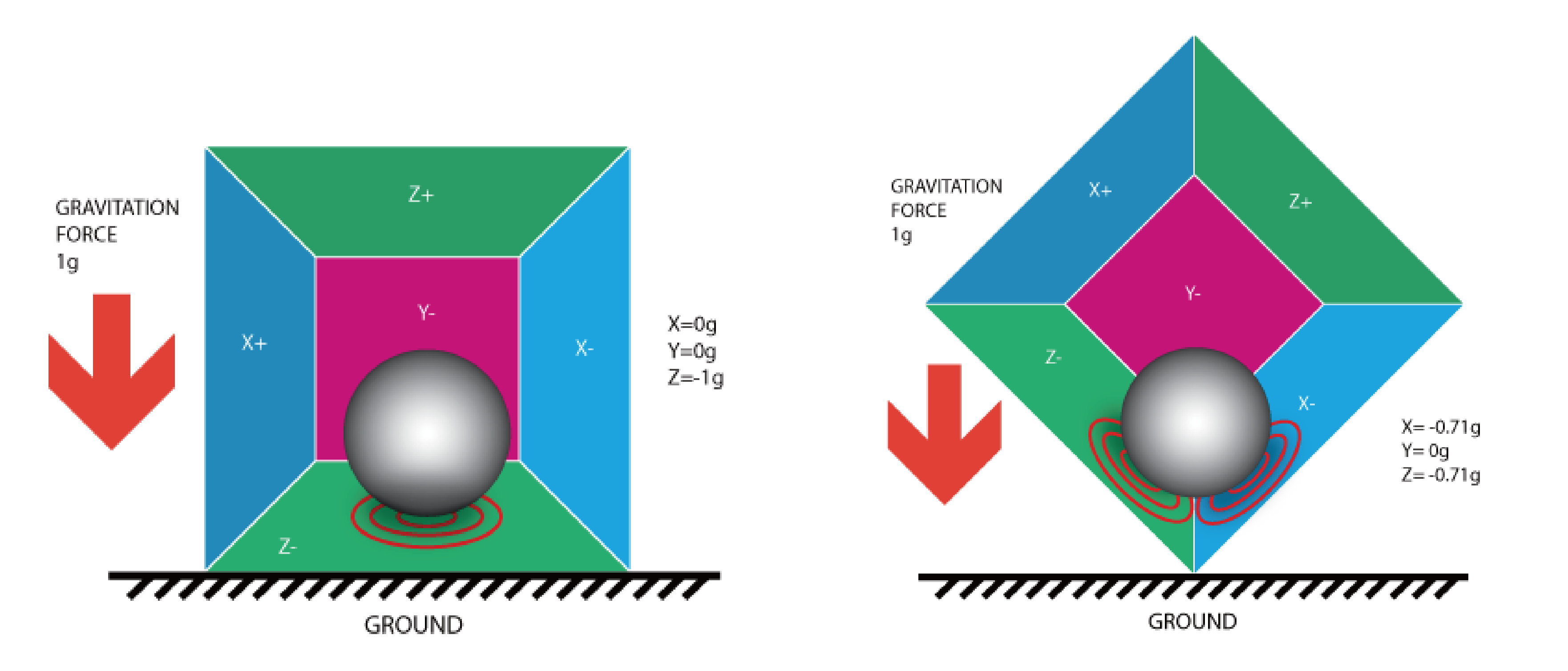
根据IMU的测量原理可知，加速度计测量的是底座对于质量块作用的力所产生的加速度。当模块处于静止时，质量块会受到向下的重力加速度，而加速度计的底座向质量块提供相反的加速度使质量块保持静止，因此在静止条件下加速度计会测量到1g竖直向上的加速度。当模块倾斜且保持静止时，可以通过重力加速度在另外一个/两个轴线上的分量计算得到模块的姿态角度：

另一方面，由于角速度是角度的导数，通过对角速度积分也可以得到姿态角：

虽然可以从加速度和角速度分别解算出角度，但这两种方式都存在很大的问题。一方面由于加速度计容易受到振动的影响，噪声很大，所以解算角度的噪声也很大，同时加速度解算的角度仅适用于静态过程；另一方面虽然陀螺仪测量角速度的噪声不是很大，经过积分环节后噪声进一步被变小，但由于初始角度并不能准确得到，而且角速度存在零漂问题，经过积分后误差会被累积。因此，两种方式解算出来的角度都无法直接使用，但我们可以采用数据融合的方法，把两种角度融合在一起，得到一个既没有累计误差、噪声又小的角度数据。

互补滤波

一阶互补滤波是最简单但却非常实用的数据融合算法，它把由加速度解算的角度和由角速度积分的角度按照一定比例加到一起，公式如下：

其中参数K表示对加速度解算角度的置信程度，由于加速度的噪声很大，所以参数K一般很小，典型值为0.05，实际使用要根据效果来调整。互补滤波器可以看做是一个高通滤波和一个低通滤波的叠加：公式的第一项是为低通滤波部分，目的是滤除加速度的噪声；公式的第二项为高通滤波部分，目的是滤除角速度的直流偏置（零漂）。

互补滤波容易理解，实现简单，运算量低；滤波器只有一个参数，所以比较容易调整；经过简单的传感器校准后，在大部分应用场景下都能取得比较好的效果。若需要更高的动态性能，可以考虑使用卡尔曼滤波。

卡尔曼滤波

卡尔曼滤波通过构建线性模型下的最优滤波器实现对IMU的数据融合与姿态解算，其中状态变量设置为角度和角速度的偏置：

状态空间模型考虑带控制量的形式，并建立为如下形式，其中状态方程的控制量为陀螺仪测量的角速度，观测方程的观测量为加速度解算得到的角度：

其中矩阵Q和R分别为输入噪声矩阵和观测噪声矩阵，是滤波器的可调参数，表征模型与测量的准确性。由加速度计观测角度的噪声较大，同时动态过程中加速度解算的角度并不准确，所以对于本问题矩阵R的参数要比Q的参数大很多。

下面给出卡尔曼滤波的递推公式，关于对卡尔曼滤波的理解，可以参考其他博客。

状态方程：

状态一步预测：

状态更新：

Arduino下的实现代码

本部分介绍如何在Arduino下实现IMU的数据融合与姿态计算，分别通过一阶互补滤波和卡尔曼滤波进行实现。对于卡尔曼滤波器，目前网络博客上的嵌入式代码更多采用数组元素的加减乘除操作，来实现矩阵的各种运算，对于初学者来说增加了一定的难度。本文调用了Arduino的矩阵运算库来实现卡尔曼滤波器，执行上会增加一定的计算量和运算时间，但更方便初学者理解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <BasicLinearAlgebra.h>
#include "math.h"
using namespace BLA;

float dt      = 0.005;
float Q_angle = 0.001;
float Q_gyro  = 0.003;
float R_angle = 0.5;
float K1      = 0.05;

float Angle_Kalman, Bias_Kalman, Angle_FOCF;

BLA::Matrix<2,1> X = {0,0};
BLA::Matrix<1,1> Y = {0};
BLA::Matrix<1,1> U = {0};
BLA::Matrix<2,2> A = {1,dt,0,1};
BLA::Matrix<2,1> B = {dt,0};
BLA::Matrix<1,2> C = {1,0};
BLA::Matrix<2,2> P = {0.1,0.1,0.1,0.1};
BLA::Matrix<2,1> K = {0.1,0.1};
BLA::Matrix<2,2> Q = {Q_angle,0,0,Q_gyro};
BLA::Matrix<1,1> R = {R_angle};

void calIMU()
{ 
  // Get IMU Raw Data
  IMU.getMotion6(&ax, &ay, &az, &gx, &gy, &gz);  //获取MPU6050陀螺仪和加速度计的数据
  // Convert Data to right unit
  gyro = gx*250.0/32767,accel_z= az*2.0*9.8/32767;
  // Calculate angle directly by two methods
  accel_angle = atan2(ay,az)*180.0/PI, gyro_angle += (gyro+1)*dt;
  // One-Order Complementary Filter
  Fist_Older_Complementary_Filter(gyro,accel_angle);
  // Kalman Filter
  Kalman_Filter(gyro,accel_angle);
  // Send Data to PC
  ANO_DT_Send_Senser(gyro*100, accel_z*100, accel_angle*100, gyro_angle*100, Angle_FOCF*100, Angle_Kalman*100, Bias_Kalman*100,0,0);
}

void Fist_Older_Complementary_Filter(float Gyro, float Accel_Angle)
{
  Angle_FOCF = K1*Accel_Angle + (1 - K1)*(Angle_FOCF + Gyro * dt);
}

void Kalman_Filter(float Gyro, float Accel_Angle)
{
  U(0,0) = Gyro;
  Y(0,0) = Accel_Angle;
  
  X = A*X + B*U;
  P = A*P*~A + Q;
  K = P*~C*((C*P*~C+R).Inverse());
  X += K*(Y - C*X);
  P -= K*C*P;

  Angle_Kalman = X(0, 0), Bias_Kalman = X(1, 0);
}

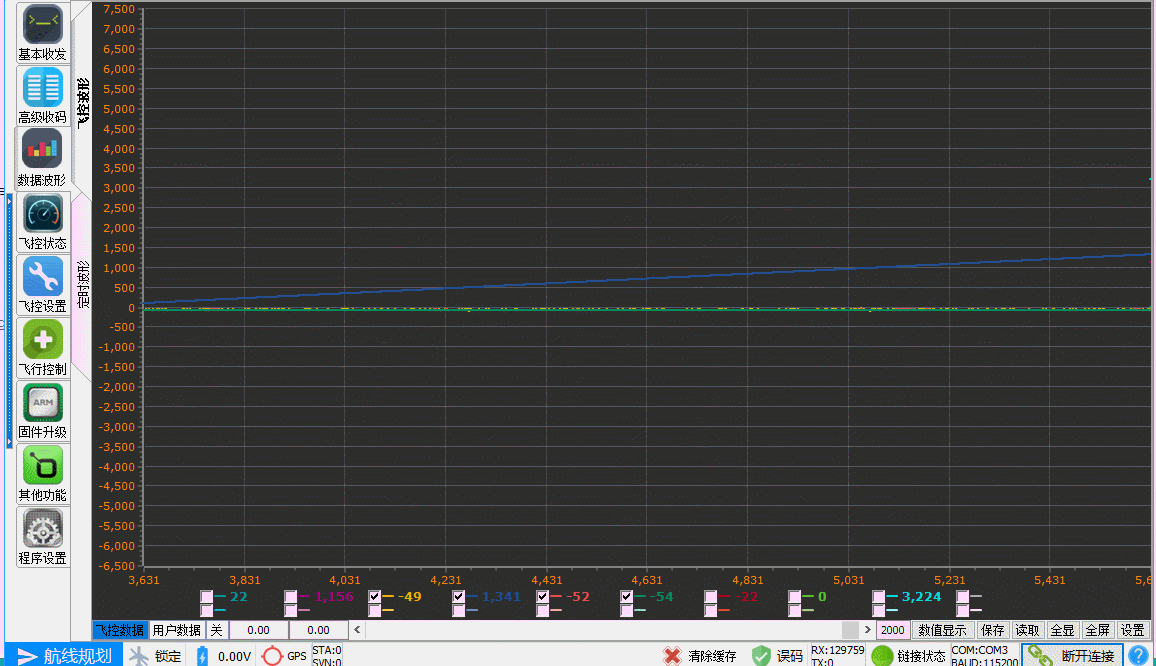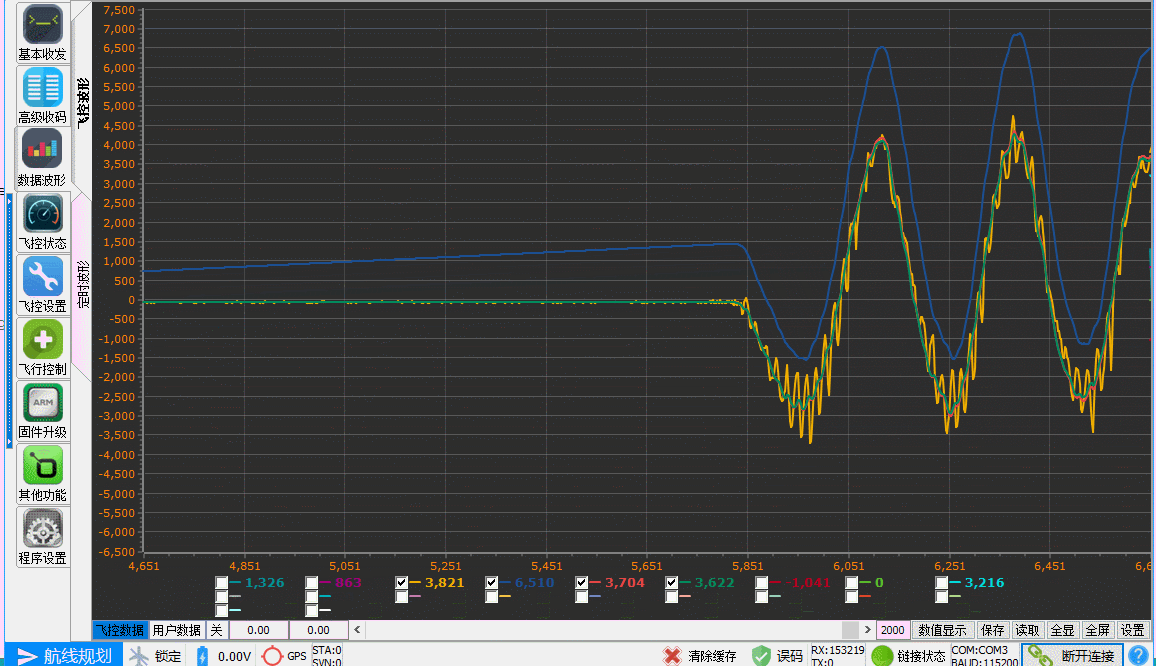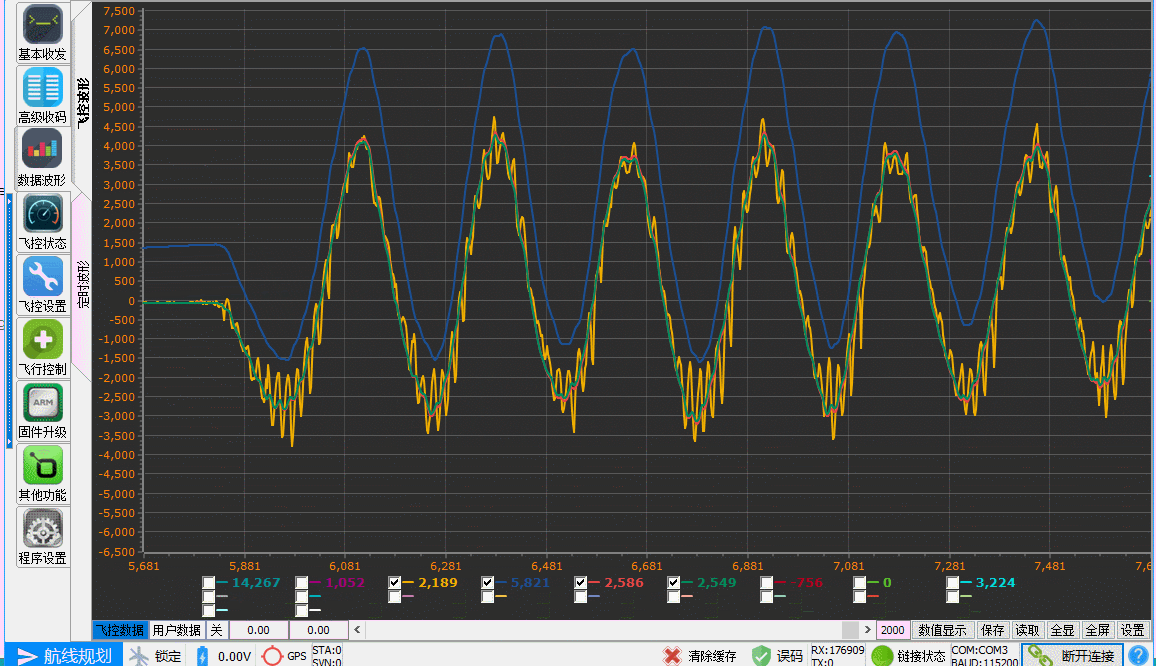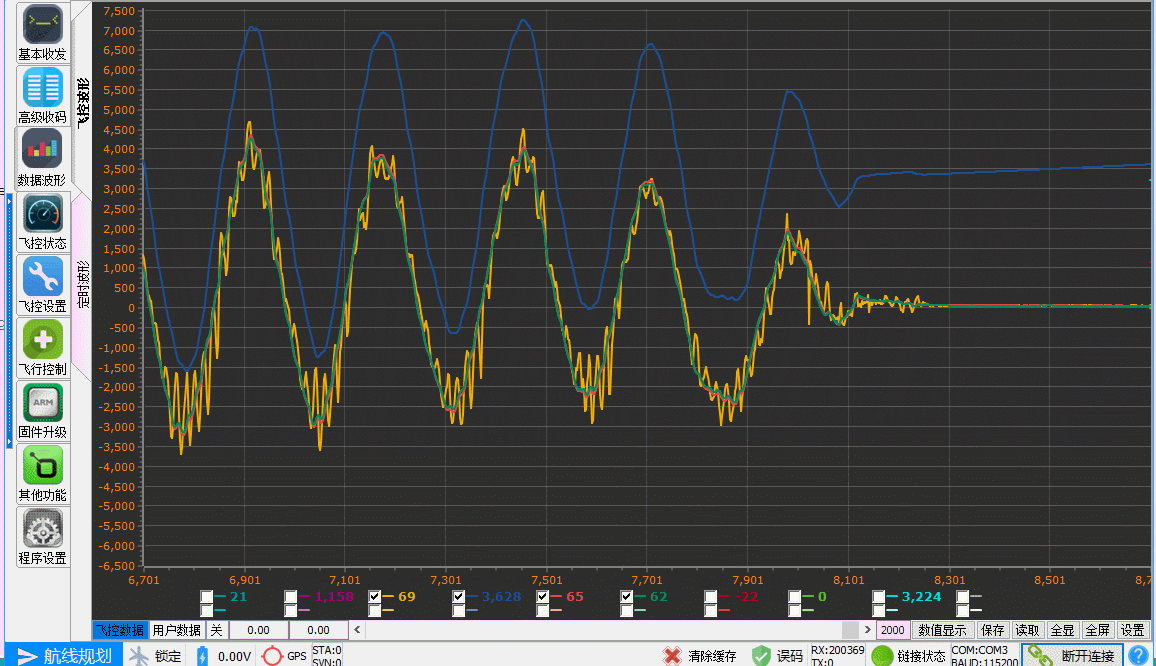
单轴姿态解算的效果如下，其中黄色为加速度计解算的角度，蓝色为陀螺仪积分得到的角度，红色和绿色分别为一阶互补滤波和卡尔曼滤波的角度曲线。在Arduino Nano平台下，输出频率为200Hz，实测单次解算耗时约3.2ms。完整的解算代码可在此处下载。

GIF 2021-3-31 14-42-51