阻抗控制 | 萤火

Hogan的三篇阻抗控制论文算是阻抗领域的经典之作，其最大贡献在于突破了原有的位控、力控的单一性，将位置、力的动态关系作为控制目标，非常适合需要与环境进行交互的控制。

根据个人浅显的理解，对论文进行一点总结。

Part I Theory

当我们谈到interaction的时候，我们主要关注交互过程的运动和力，以及两者的乘积-交互过程的能量流动。在一些情况下，交互过程能量流动可以被近似忽略，而交互控制也因此可以被简化。例如在交互力很小的情况下（例如喷涂），可以采用纯位置控制；在作用力方向上没有位移的情况下（例如焊接），可以采用力位混合控制。在余下大部分的情况下，交互过程往往都伴随着能量的转移，这时候单一的控制量（位置、速度、交互力）就不足以控制交互过程能量流动。

这个问题的一个解决方法是，控制操纵器的动态行为。如果将环境视作为操纵器的扰动，通过调节操纵器对扰动的响应则可实现对于动态行为的控制。这种调节不是通过动态调整控制器的参数（如改变pid的参数），而是通过探索物理交互的本质特性来实现的。

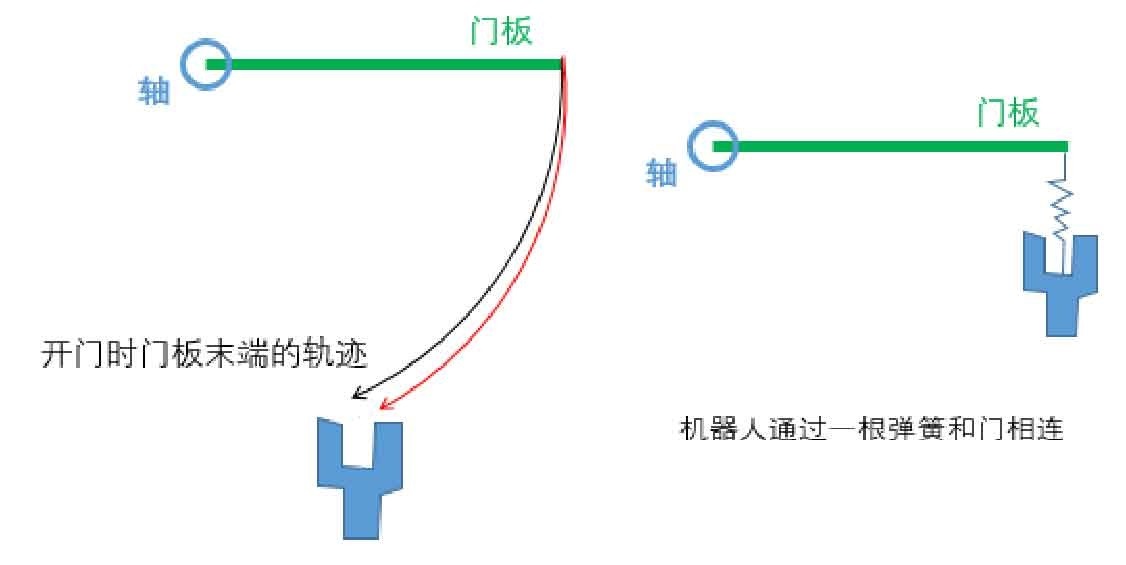
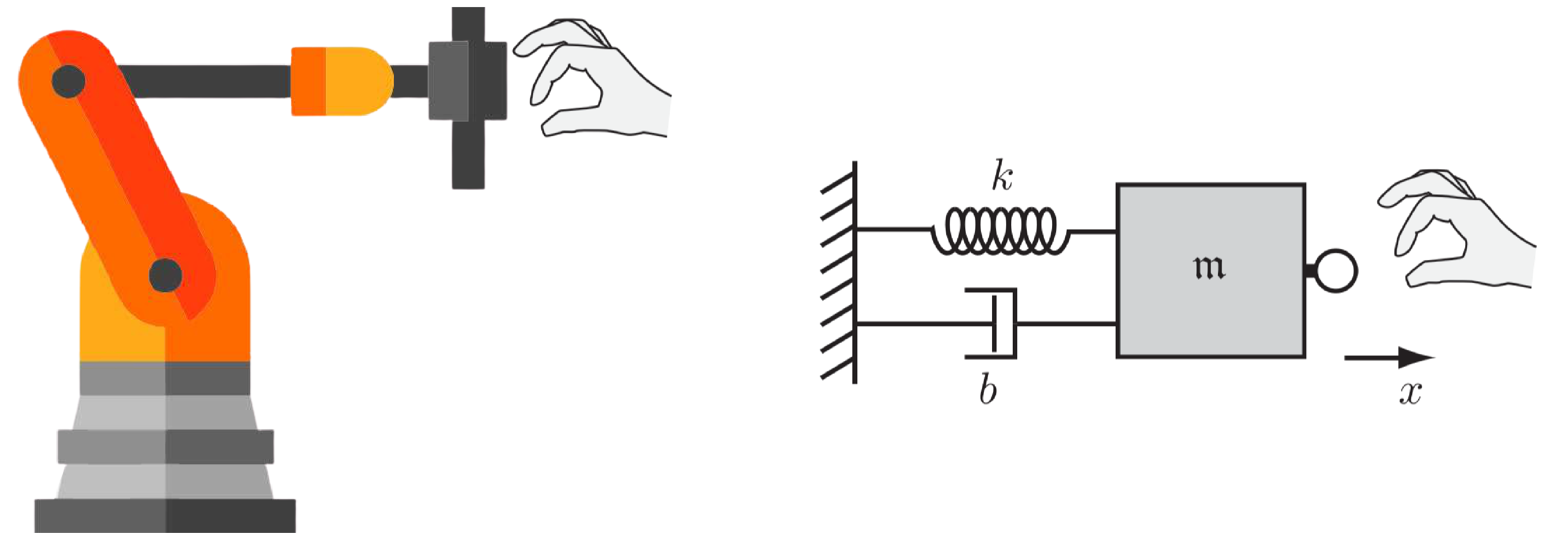
借用知乎邵天兰关于机械臂开门的例子来做一个形象的解释。假定让机械臂去完成开门这个动作，由于门框的轴对门板产生了一定的运动学约束，门板的末端只能按照固定的轨迹进行运动。当采用完全的位置控制时，由于机械的规划轨迹和门的轨迹不可能做到完全一致（定位误差、传感器精度等诸多限制），这些偏差会使得门板和机械臂之间产生巨大的交互力；而若采用完全的力控，门板正常转动时的交互力又很小，很难实现较为准确的开门角度；因此必须要同时考虑位置和力的共同影响，才能较好的实现开门这个动作。实际上这样一个简单又复杂的问题，可以通过在机械臂末端添加一个弹簧来解决，机械臂采用位置控制时，弹簧的柔顺性使得即便存在一定的位置误差也不会产生很大的交互力。而阻抗控制，就是通过控制算法使机械臂表现出这样的弹簧行为。

物理等效性

操纵器是是物理硬件（机械结构、传感器、驱动器）和软件算法（控制程序）集合而成。一个统一的框架应当将硬件和软件一同纳入其中。在Hogan的观点中，硬件和软件共同作用下的操纵器，在与环境的交互中应当表现正常物理系统应当具有的特性，也就是说，软件部分所代表的控制器，也应当具有适当的物理特性：

It is impossible to devise a controller which will cause a physical system to present an apparent behavior to its environment which is distinguishable from that of a purely physical system.

这就是阻抗控制最核心的思想，控制器不再是一个完全虚拟的概念，而是可以等效为一定物理模型，具有一定的物理特性。从另一角度来说，控制器不再是任意设计的，而受到一定的物理特性的约束。在此基础上，Hogan进一步对交互过程的两种方式，impedance和admittance，进行进一步阐述。

因果关系

在任意一个运动的自由度上，瞬时功率都由两项相乘而得：effort（例如力、电压）和flow（例如速度、电流）。任何一个物理系统在任意一个时刻都只能控制着两者中的一个，而不能控制两者全部（Hogan在这里更主要的是强调单自由度-单输入单输出的情况，最优控制问题也并未与此矛盾）。

因此从交互的能量视角出发，物理系统可以看做只存在两种类型：admittance和impedacne，其中admittance接受effort而产生flow，而impedance接受flow而产生effort，这两者有点类似于电学系统中的电阻和电导。但不同于电学系统，admittance和impedance一般是不能互换的，例如是因为速度而产生的摩擦力，而不能说是因为摩擦力而产生了速度。这种非相互转化的特性是因果关系的体现，对于一个确定的物理关系而言，例如$F=ma$，尽管从数学上可以从右到左去表达，但实际物理系统只能从左到右与产生。这种因果关系表明，对于任意一个物理系统，它只能被描述为admittance或impedance中确定的一种特性（这种确定应当是相对的）。

The most important consequence of dynamic interaction between two physical systems is that one must physically complement the other: Along any degree of freedom, if one is an impedance, the other must be an admittance and vice versa.

在交互过程中我们希望交互过程可以表现的比较柔顺“compliance”，交互力的变化比较平滑。为实现柔顺交互，进行交互的两个物理系统必须是物理互补的，即其中一个若表现出admittance，另一个则必须为impedance。在非互补的两种情况下，可能会导致非柔顺的交互过程（admittance-admittance），或者物理不可实现（impedance-impedance）。

对于大部分的操纵任务而言，其环境多少会包含惯性约束或运动学限制，这样的环境接收力的输入，然后产生运动响应（当然也可能没有运动），这样的物理特性只能看做是admittance。因此，与这样的环境进行交互时，操纵器必须表现出impedance，才能实现柔顺交互。

接下来进一步讨论如何将impedance和admittance用物理模型和数学方法进行表示。由于Hogan的论文中较多的是文字描述，公式较少，且采用的bond graphs也不为控制领域所熟悉，因此下一部分将主要参考Unified Impedance and Admittance Control以及Modern Robotics - Mechanics, Planning, and Control中的内容进行介绍。

Part II Algorithm and Implementation

模型

考虑一个非常简单的单自由度惯性系统，系统的动力学方程可以表示为如下形式：

$m\ddot{x} = F+ F_\mathrm{ext} \quad\quad(1)$

$F_\mathrm{ext}$表示环境提供的交互力，注意这个公式是对于真实系统的建模，对于复杂的交互系统可以建立更加复杂的模型。

无论是impedance control还是admittance control，其控制算法的设计目的都是通过控制操纵器的输出力$F$，使得外部力$F_\mathrm{ext}$与期望位置偏差$e=x-x_0$能够满足一定的关系，或者说外部力在与操纵器进行交互的时候具有一定的物理特性，如下图所示。区别于上面的动力学方程，这种物理特性是虚拟出来的，没有实际物理存在。一般来说，较多的采用二阶模型：

$M_d \ddot{e}+D_d \dot{e}+K_de=F_{\mathrm{ext}} \quad\quad(1)$

式中$M_d$，$D_d$，$K_d$分别表示期望惯性、阻尼、刚度。在这样的关系下，外部力在与操纵器交互的时候，就像是在推动一个有阻尼、弹簧连接的质量块一样。由于这样一个关系是完全虚拟出来的，因此式中的三个参数可以任意调整。其中，刚度参数$K_d$是最重要的，也是最主要调节的参数，它反映操纵器的刚度大小，直接决定操纵器在与环境接触吋是呈现刚性还是柔性。一般来说，减小$K_d$会使机械手与环境的接触力变小，增大则会使机械臂与环境的接触力变大。阻尼参数$D_d$的增大或减小一般不会使接触力的稳定值变化，但可以调节操纵臂与环境交互的动态过程。一般来说，增大$D_d$会使力响应的超调减小，交互力的峰值显著下降，但过大的阻尼会使力响应过程变慢。惯性参数$M_d$一般不需要进行调节，但需要根据任务适当的进行选取。当这三个参数有任意一个的值较大时，我们其称为high impedance；若三个参数都很小时，称为low impedance。

进一步，可以对上式进行Laplace变换：

$(M_ds^2+D_ds+K_d)E(s)=F_\mathrm{ext}(s)$

由此可以通过位置扰动到外部力的传递函数来定义impedance：$Z(s)=F_\mathrm{ext}(s)/E(s)$，这样impedance就是一个与频率相关的概念，低频时的响应主要由弹性项决定，而高频时的响应主要由惯性项决定；而admittance就可以定义为impedance的逆：$Y(s)=z^{-1}(s)=X(s)/F(s)$。

一个好的位置控制器应当是high impedanc - low admittance，由于$E(s)=Y(s)F_\mathrm{ext}(s)$，来自外部力的扰动才能较小的影响位置；同理好的力控制应当是low impedance - high admittance，外部位置的扰动对力的影响才会比较小。从这一点来说，无论是位置控制还是力控制，都可以看做是阻抗控制的特例，是阻抗为无穷大和无穷小下的具体实现。

Impedance Control

由于impedance的性质是接受flow而产生effort，因此一个impedance controller应当是以位置信息作为输入，以力的信息（关节力矩）为输出。考虑公式（1）与公式（2），得到如下的impedance控制系统：

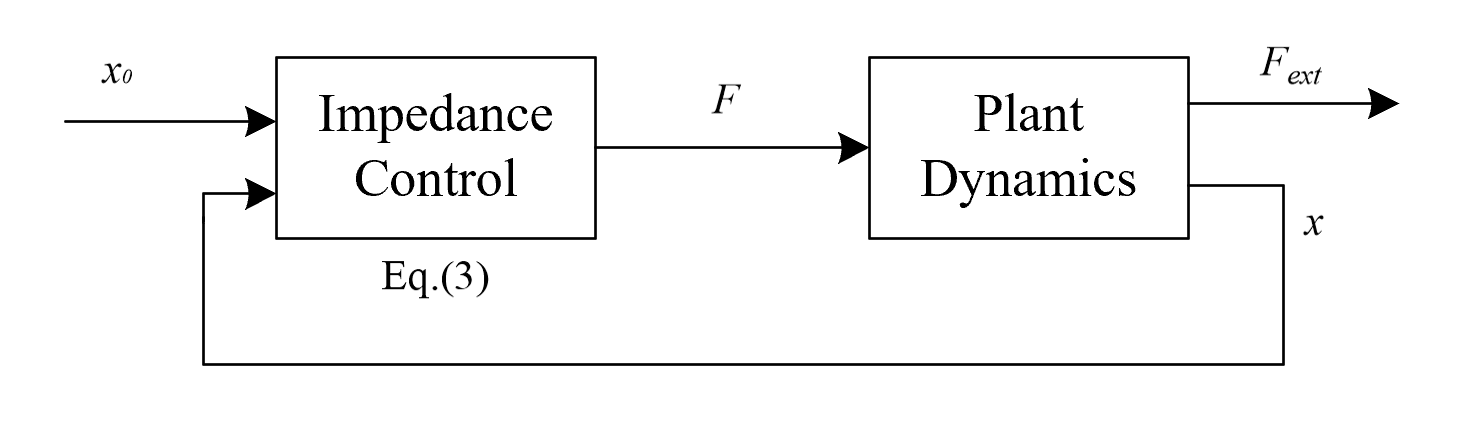
$F=m\ddot x - \left( M_d \ddot{e}+D_d \dot{e}+K_d e \right) \quad\quad(3)$

有时候公式（3）中的加速度，包括$\ddot x$和$\ddot e$，比较难测量，可以通过测量$F_{ext}$来进行简化：

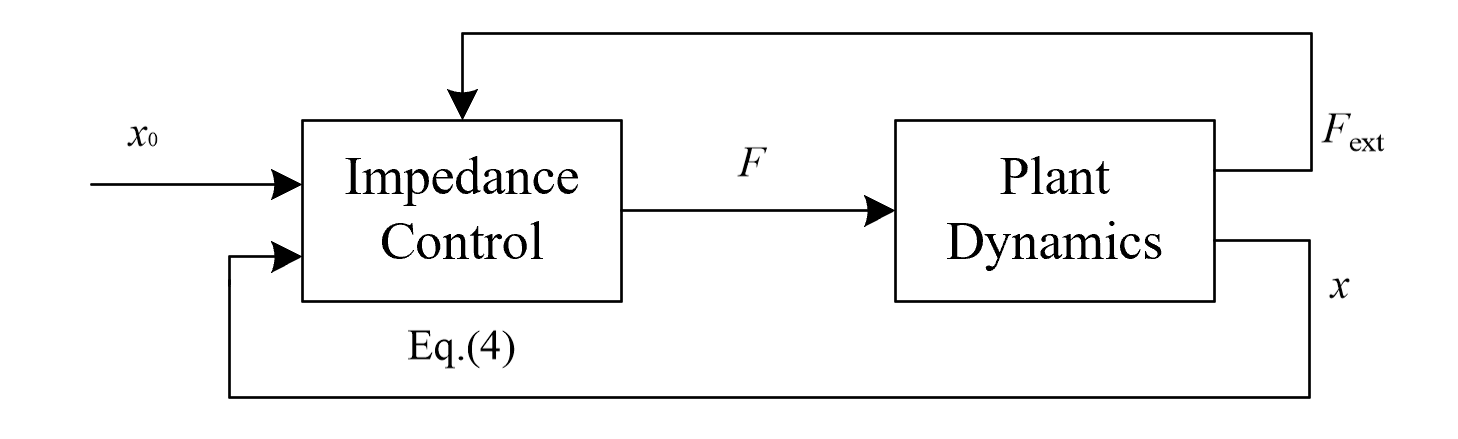
$F=\left(\frac{m}{M_d}-1\right) F_{\mathrm{ext}}+m \ddot{x}_{0}-\frac{m}{M_d}\left(D_d \dot{e}+K_d e\right) \quad\quad(4)$

Admittance Control

admittance接受effort而产生flow，因此admittance controller应当是以测量的交互力作为输入，以位置指令作为输出。一种简单的实现方法可以通过计算期望的加速度来得到：

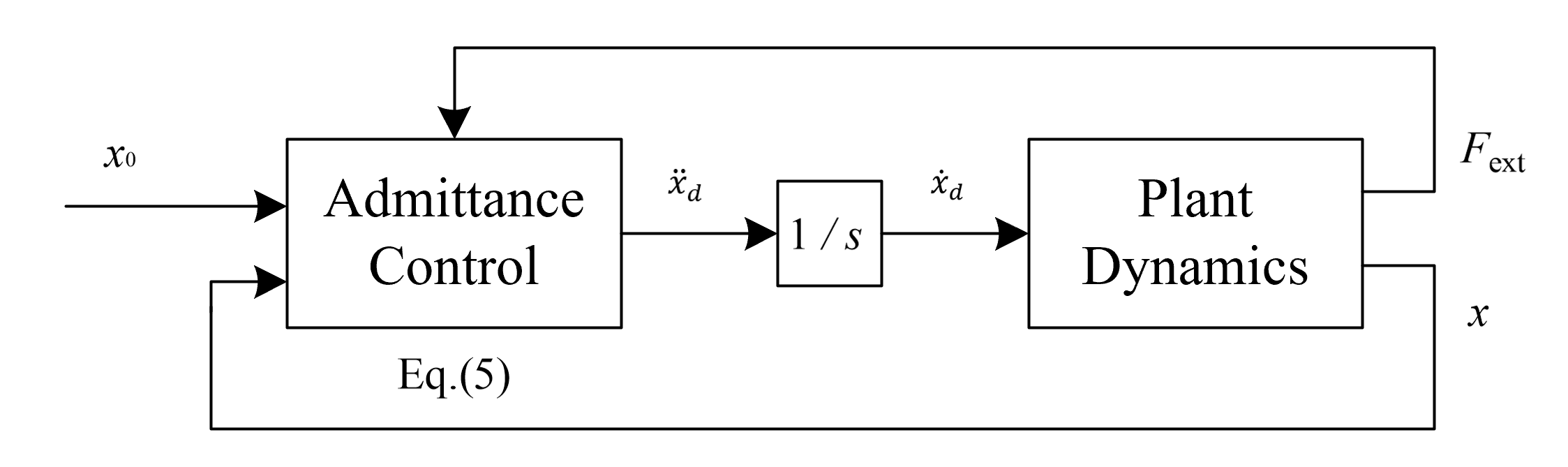
$M_d \ddot{e}_d+D_d \dot{e}+K_de=F_{\mathrm{ext}}$ $\ddot{x}_d = \ddot{x}_\mathrm{0} +\frac{1}{M_d}(F_{\mathrm{ext}}-D_d \dot{e}-K_d e ) \quad\quad(5)$

这两种控制方式各有利弊，可以看出impedence control方法可以不用测量交互力的数据，但需要知道系统的动力学模型，这种方法在与环境交互的时候稳定性（柔顺性）比较好的，但无接触时实际上为开环系统，位置控制精度受制于建模精度；admittance control方法不需要进行系统动力学建模，在伺服任务中有较高位置精度，但与同样是admittance的环境交互时柔顺性较差，系统容易不稳定。

在实际的使用中，impedance/admittance control的实现方式远不止上面几种，根据系统的硬件结构、测量数据、反馈信号、工作空间的不同，可以设计各种形式的impedance controller。以机械臂为例，我们可以将机械末端笛卡尔坐标系下的阻抗模型通过雅克比矩阵转化到关节空间下进行实现：

$\tau=J^{\mathrm{T}}(\theta)\left(\underbrace{\tilde{\Lambda}(\theta) \ddot{x}+\tilde{\eta}(\theta, \dot{x})}_{\text {arm dynamics compensation }}-\underbrace{(M \ddot{x}+B \dot{x}+K x)}_{f_{\text {ext }}}\right)$

以上就是Impedance Control在控制领域的具体实现。实际上Impedance的概念可以应用到诸多领域，下面一部分将主要介绍Impedance与人体运动。

Part III - Impedance and Human Movement

人体的运动系统是这世界上最神奇的事物之一。在神经肌肉骨骼的共同作用下，人类得以实现无比丰富而复杂的动作，得以使用和制作各种工具，从而由古猿进化为智人，进化为这颗星球上最具智慧的生命。人体的运动千变万化，既有舞蹈那般的优雅流畅，又有雕刻那样准确精细；既有举重那般爆发力量，又可如武术那样灵巧迅捷。千百年来，人们试图去理解人体运动的本质，理解神经系统运动控制的机制，从而实现更加拟人的机器人运动与人类相协同，从而设计更智能的假肢帮助残疾人恢复运动功能。Impedance就是这样一种理解人体运动的方式。

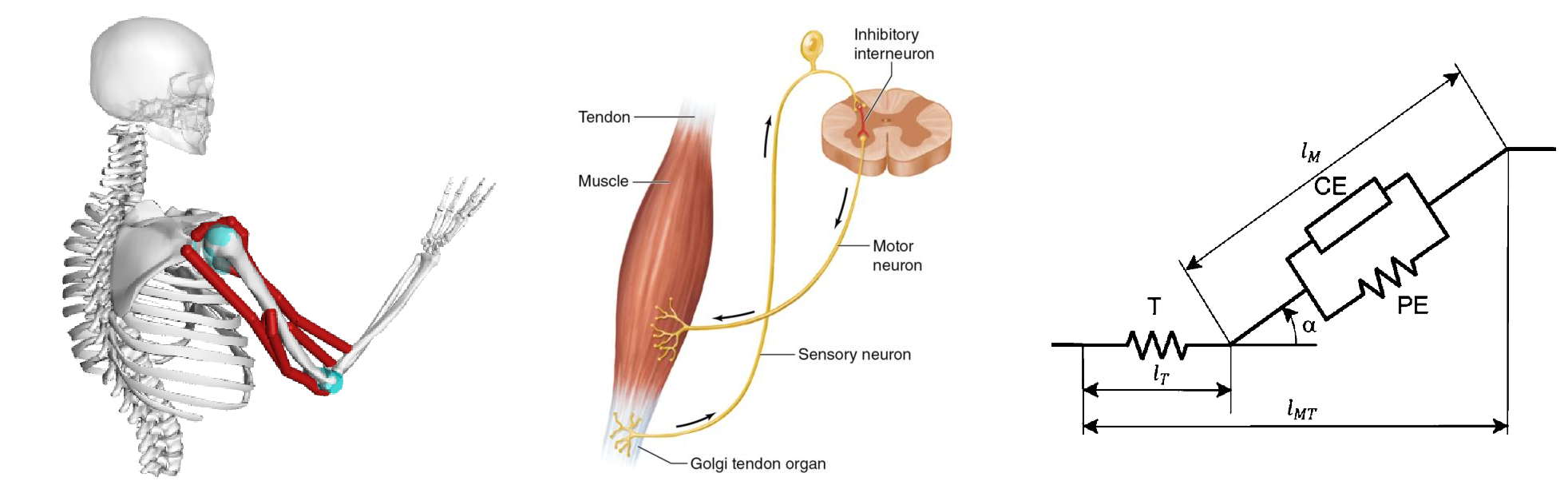
人体的运动系统由神经-肌肉-骨骼共同构成，神经信号刺激肌肉收缩，肌肉收缩带动骨骼运动。尽管人体的肌肉并不是能量保守的，但却具有很明显的阻抗特性，Hill肌肉模型就是将肌肉表示为收缩单元与串联弹簧与并联弹簧的组合，人体的驱动器-肌肉本身就类似于SEA；而用来表示肌肉收缩动力学的力-长度与力-速度关系，则可以看作是阻抗控制中的刚度参数和阻尼参数。

由于肌肉只能单向驱动一个关节，因此为了实现关节层次的阻抗调节，需要相对立的两块肌肉共同收缩，这在生理学上称为Cocontraction of antagonistic muscle groups。想象着你从空中跳跃而下，在接触地面之时你需要保持腿部各关节的肌肉收缩来实现关节刚度的增加，以避免不必要的伤害；再考虑球场上你面对传来的篮球，下意识增加手腕处对立肌肉的收缩，从而能稳稳地接住它。通过调节关节阻抗来对抗环境的不稳定，是人体生理神经系统的基本准则；而通过学习利用自身或环境的动力学、减少不必要的阻抗和肌肉消耗，是我们适应这个世界基本方式。

当从阻抗的角度去理解人体运动时，能够得到比直观想象更是深刻一些的思考。人体肌肉系统一个特点是具有高度冗余，连接一个关节两侧骨骼的肌肉远远多于驱动该关节所必须的肌肉，甚至存在很多跨越多个关节的肌肉，例如上肢中最简单的肘关节就是由肱肌、肱桡肌、二头肌短头和二头肌长头共同作用。这种肌肉系统的冗余与复杂性对于阻抗控制来说起到什么作用？

Muscle Redundancies

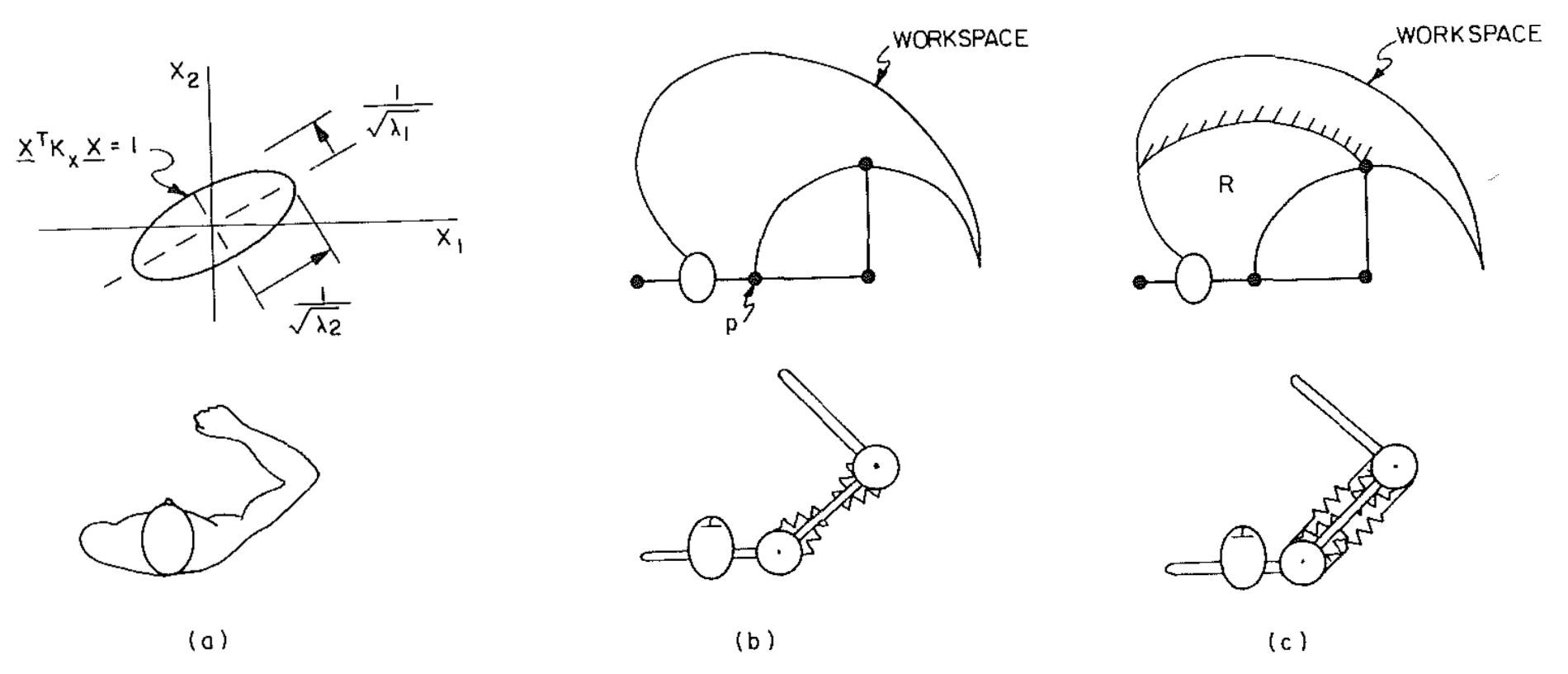
考虑由大臂、小臂和躯干组成的二连杆模型在平面进行运动的情况，如图(a)所示。将手部视为刚体并忽略腕关节的自由度。为简化分析，将肌肉用弹簧进行描述，弹簧的刚度系数可以由神经信号进行调整。首先研究只有单关节肌肉的情况，图(b)所示。记相对关节角度为$\rho_1$,$\rho_2$，肩关节和肘关节的刚度系数分别为$K_s$,$K_e$，则关节力矩可以表示为如下形式：

$\left[\begin{array}{c} T_{1} \\ T_{2} \end{array}\right]=\left[\begin{array}{cc} K_s & 0 \\ 0 & K_e \end{array}\right]\left[\begin{array}{l} \rho_{1} \\ \rho_{2} \end{array}\right]$

式中的矩阵称为刚度矩阵，反应关节阻抗特性。由于我们更关心末端执行器-手部，与环境交互时的阻抗特性，因此进一步将上面的阻抗关系变化到笛卡尔坐标下。考虑相对关节角度与绝对关节角度之间的变化关系：

$\left[\begin{array}{c} \rho_{1} \\ \rho_{2} \end{array}\right]=\left[\begin{array}{rr} 1 & 0 \\ -1 & 1 \end{array}\right]\left[\begin{array}{l} \theta_{1} \\ \theta_{2} \end{array}\right] = T\left[\begin{array}{l} \theta_{1} \\ \theta_{2} \end{array}\right]=K_\theta \theta$

绝对关节角坐标系下的阻抗关系为：

$\left[\begin{array}{c} T_{1} \\ T_{2} \end{array}\right]=T^T\left[\begin{array}{cc} K_s & 0 \\ 0 & K_e \end{array}\right]T\left[\begin{array}{l} \theta_{1} \\ \theta_{2} \end{array}\right] =\left[\begin{array}{cc} K_s+K_e & -K_e \\ -K_e & K_e \end{array}\right]\left[\begin{array}{l} \theta_{1} \\ \theta_{2} \end{array}\right]$

末端位置到关节角度的雅克比矩阵为：

$J=\left[\begin{array}{cc} -L_{1} \sin \theta_{1} & -L_{2} \sin \theta_{2} \\ L_{1} \cos \theta_{1} & L_{2} \cos \theta_{2} \end{array}\right]$

关节阻抗到末端阻抗的变换关系为：

$\tau=J^TF \Rightarrow K_\theta d\theta = J^TK_x dx \Rightarrow K_\theta = J^TK_x J \Rightarrow K_x = (J^T)^{-1}K_\theta J^{-1}$

假定$L_1=L_2=1$，并令$\Lambda=C_1S_2-S_1C_2$，则有：

$K_x = \frac{K_s}{\Lambda^2} \left[\begin{array}{cc} C_2^2 & S_2C_2\\ S_2C_2 & S_2^2 \end{array}\right]+ \frac{K_e}{\Lambda^2} \left[\begin{array}{cc} (C_1+C_2)^2 & (S_1+S_2)(C_1+C_2)\\ (S_1+S_2)(C_1+C_2) & (S_1+S_2)^2 \end{array}\right]$

虽然在相对关节角度坐标系下刚度矩阵是对角的，但在末端笛卡尔坐标系下刚度矩阵一般不再具有对角性。通过调节关节刚度$K_s$和$K_e$，可以实现对末端笛卡尔坐标系下的阻抗调节，且肌肉的冗余度越高，则对于阻抗的调节就越灵活。但由于刚度矩阵有三个自由变量（对称性），因此调节$K_s$和$K_e$无法实现任意形式阻抗模式。考虑当$\theta_1=0, \theta_2=90^{\circ} $时，$\Lambda=1$，$K_x$可以表示为如下形式：

$K_x = {K_s} \left[\begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right]+ {K_e}\left[\begin{array}{cc} 1 & 1\\ 1 & 1 \end{array}\right]$

上式表明无论人体如何调整关节的刚度系数或是肌肉的收缩程度，都不可能使末端笛卡尔坐标下的刚度矩阵等于单位矩阵。若进一步用刚度椭圆来表示表示刚度矩阵（长轴和短轴分别代表刚度矩阵的两个特征值，长轴和短轴的方向分别为特征向量的方向），可以看出随着关节刚度的调节，末端笛卡尔坐标系下刚度椭圆的长轴只能够在如下深蓝和深红两条虚线内变化。在这样的阻抗特性下，手臂末端更容易对抗平行于蓝色虚线的扰动，而容易收到垂直于蓝色虚线的扰动的影响；也就是说在这样的阻抗特性下，你会很容易写出丿，却很难写出㇏。

现在向这个二连杆机构引入双关节肌肉，在双关节肌肉和单关节肌肉的共同作用下，相对关节角度坐标系下的阻抗特性如下：

$\left[\begin{array}{c} T_{1} \\ T_{2} \end{array}\right]=\left[\begin{array}{cc} K s+K t & K t \\ K t & K e+K t \end{array}\right]\left[\begin{array}{l} \rho_{1} \\ \rho_{2} \end{array}\right]$

将其变换到末端笛卡尔坐标系下，可得：

第三个参数$K_t$增加了刚度矩阵的可调节范围，甚至在一定工作空间内可以实现任意形式的阻抗特性。依然考虑$\theta_1=0, \theta_2=90^{\circ} $的情况：

$K_x = {K_s} \left[\begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right]+ {K_e}\left[\begin{array}{cc} 1 & 1\\ 1 & 1 \end{array}\right]+ {K_t}\left[\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right]$

可以看出只要取$K_s=1, K_e=0, K_t=1$就可以使$K_x$为单位矩阵，甚至当前位姿下，通过调节$K_s, K_e, K_t$几乎可以实现任意形式的刚度矩阵，末端笛卡尔坐标系下可以表现出任意形式的阻抗特性，正如下图所展示的那样。

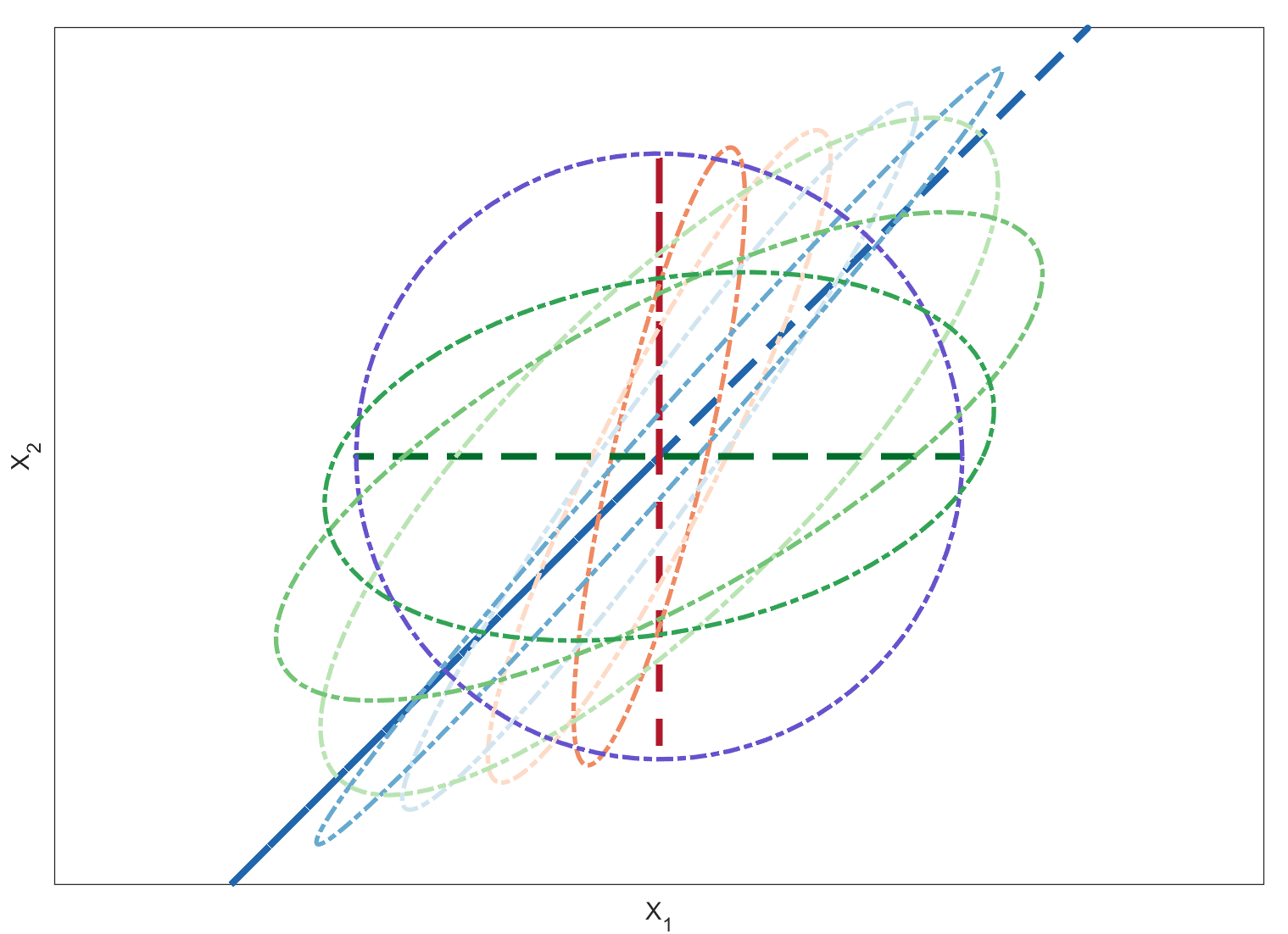
由此，人体肌肉系统的冗余与复杂是有明确意义的，这经过亿万年进化而来的肌肉系统，增加了人体阻抗-尤其是末端阻抗的可调范围，使人类尽可能少的受到自身能力的限制，能够根据需要任意调整与环境交互时的阻抗特性，灵巧的使用各种工具来拓宽其生存边界与层次。

Impedance Learning

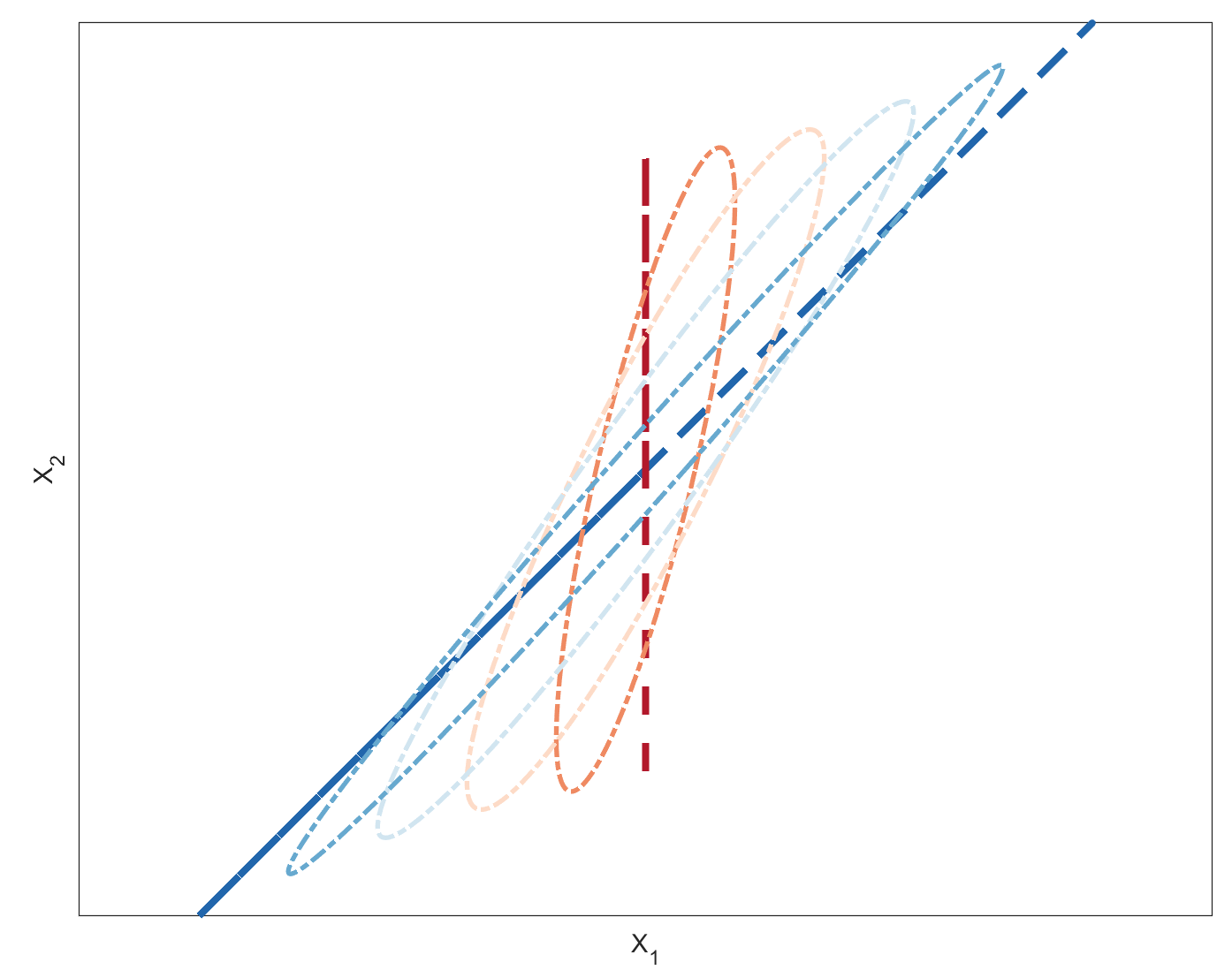
而人体的运动控制，可以很自然的看做是对于阻抗特性的学习。还是以手臂二自由度平面运动为例，在2001年的一篇Nature论文The central nervous system stabilizes unstable dynamics by learning optimal impedance中，研究人员通过与交互的机械臂在运动区域内构建了一个扩散力场（如下图所示）：当手臂末端运动偏离预定轨迹时会在$x$方向上受到干扰作用力，且随着偏差加大，作用力也越大，因此具有不稳定的特性。

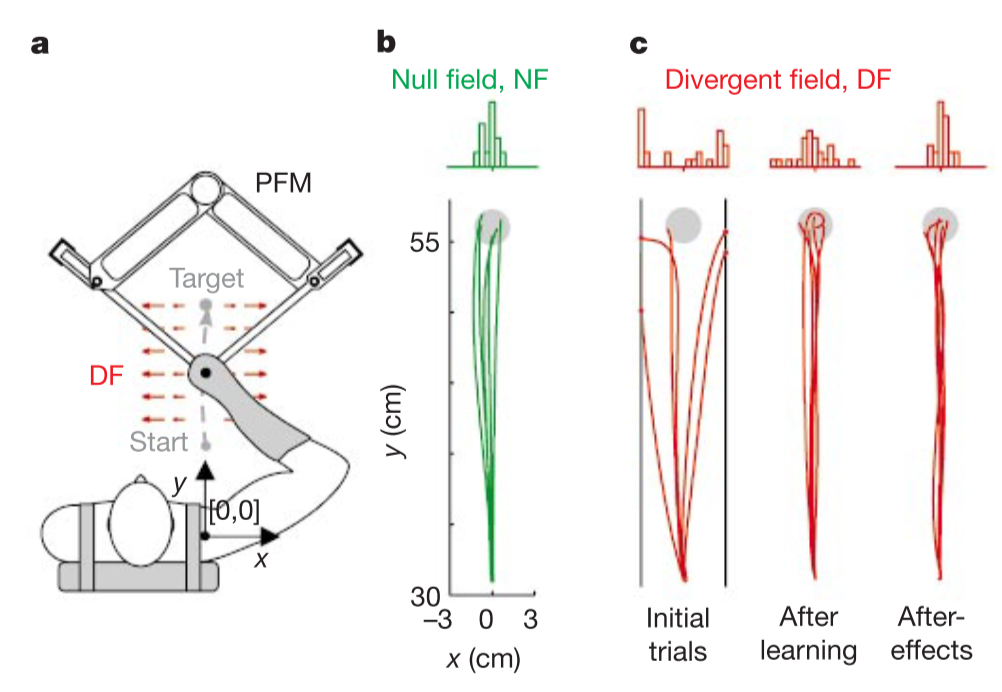
$\left[\begin{array}{l} F_{x} \\ F_{y} \end{array}\right]=\left[\begin{array}{l} \beta x \\ 0 \end{array}\right]$

研究人员令受试者分别在无力场、有扩散力场的条件下，分别控制手臂末端沿y方向进行运动。在没有力场的作用下，受试者能够实现良好的运动轨迹；在刚施加扩散力场后，受试者的运动变得不稳定，而经过一段时间的学习后，受试者恢复了良好的运动轨迹。研究人员测量了不同受试者在力场作用前后的末端阻抗特性，刚度椭圆无一例外的增加了x方向上的长度，也就是增加了x方向上的刚度系数，使得能够对抗来自x方向上扩散力场的扰动。

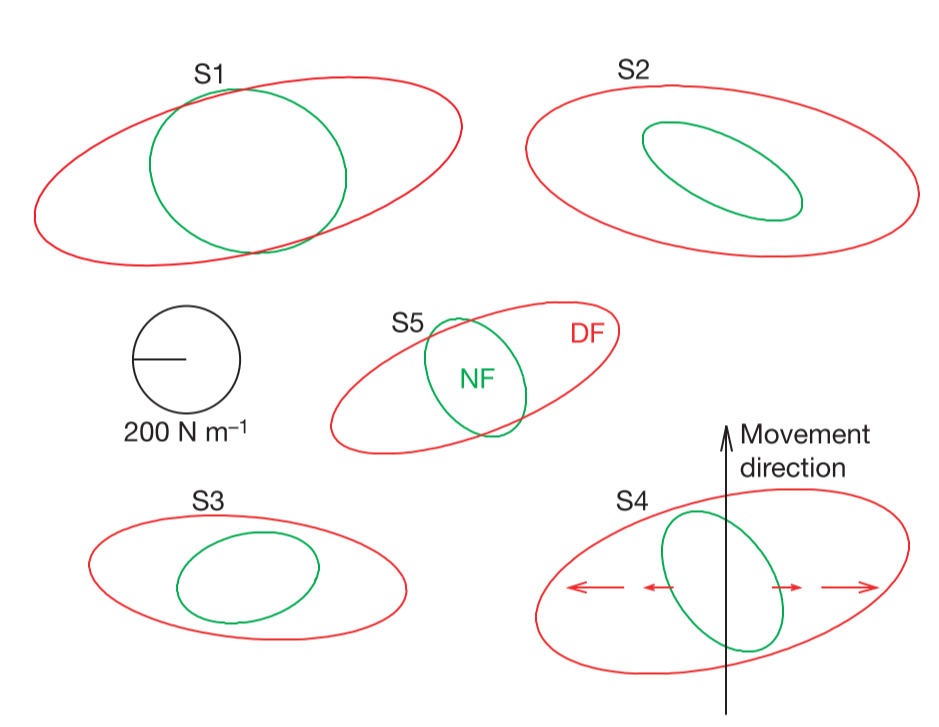
在扩散力场的作用下，人体的神经系统学会了新的阻抗特性来适应环境。类似的例子还有很多，当你骑自行车时，你用双手控制车把使车把表现出阻抗特性，使受到扰动后能恢复车把与前进方向平行；当你使用螺丝刀时，你控制螺丝刀在非法向方向上保持较高的阻抗，使得螺丝刀不会因为扰动而滑落。对于一切稳定和不稳定的环境，人体学习调整自身的肌肉表现适当的阻抗形式使交互过程保持稳定，再学习利用环境和自身的动力学特性使交互的动态过程更有效率。

因此，人体运动控制本质是对阻抗特性的控制，学习环境（外部条件）、位姿（内部状态）与阻抗之间的映射关系，学习刚（admittance）柔（impedance）之间的相互转化，学习鲁棒与最优之间的动态平衡；而最终，促成了人类丰富多彩的世界。

参考文献

Hogan N. Impedance control: An approach to manipulation: Part I—Theory[J]. 1985.
Hogan N. Impedance control: An approach to manipulation: Part II—Implementation[J]. 1985.
Ott C, Mukherjee R, Nakamura Y. Unified impedance and admittance control[C]//2010 IEEE International Conference on Robotics and Automation. IEEE, 2010: 554-561.
Kevin M.. Lynch, Park F C. Modern Robotics: Mechanics, Planning, and Control[M]. Cambridge University Press, 2017.
Milner T E. Adaptation to destabilizing dynamics by means of muscle cocontraction[J]. Experimental brain research, 2002, 143(4): 406-416.
Burdet E, Osu R, Franklin D W, et al. The central nervous system stabilizes unstable dynamics by learning optimal impedance[J]. Nature, 2001, 414(6862): 446-449.